If the coefficients of x7 and x6 in (2+x3)n are equal, then n is
56
55
48
15
The correct Answer is:c
To solve the problem, we need to find the value of n such that the coefficients of x7 and x6 in the expansion of (2+x3)n are equal.
1. Identify the coefficients:
The coefficient of xr in the expansion of (a+b)n is given by the formula:
Coefficient of xr=(nr)an−rbr
Here, a=2 and b=x3.
2. Calculate the coefficient of x7:
For r=7:
Coefficient of x7=(n7)⋅2n−7⋅(13)7
Simplifying this gives:
Coefficient of x7=(n7)⋅2n−7⋅12187
3. Calculate the coefficient of x6:
For r=6:
Coefficient of x6=(n6)⋅2n−6⋅(13)6
Simplifying this gives:
Coefficient of x6=(n6)⋅2n−6⋅1729
4. Set the coefficients equal:
According to the problem, the coefficients of x7 and x6 are equal:
(n7)⋅2n−7⋅12187=(n6)⋅2n−6⋅1729
5. Cross-multiply to eliminate fractions:
(n7)⋅2n−7⋅729=(n6)⋅2n−6⋅2187
6. Simplify the equation:
Dividing both sides by 2n−7:
(n7)⋅729=(n6)⋅2⋅2187
Since 2187=37, we can simplify further:
(n7)⋅729=(n6)⋅4374
7. Use the relationship between binomial coefficients:
Recall that:
(n7)=n!7!(n−7)!and(n6)=n!6!(n−6)!
Thus, we can express (n7) in terms of (n6):
(n7)=n−67⋅(n6)
8. Substituting back:
Substitute (n7) into the equation:
n−67⋅(n6)⋅729=(n6)⋅4374
Cancel (n6) (assuming n≥6):
n−67⋅729=4374
9. Solve for n:
Multiply both sides by 7:
n−6=4374⋅7729
Simplifying gives:
n−6=42⇒n=48
Final Answer:
Thus, the value of n is 48.
The coefficient of xr in the expansion of (a+b)n is given by the formula:
Coefficient of xr=(nr)an−rbr
Here, a=2 and b=x3.
For r=7:
Coefficient of x7=(n7)⋅2n−7⋅(13)7
Simplifying this gives:
Coefficient of x7=(n7)⋅2n−7⋅12187
For r=6:
Coefficient of x6=(n6)⋅2n−6⋅(13)6
Simplifying this gives:
Coefficient of x6=(n6)⋅2n−6⋅1729
According to the problem, the coefficients of x7 and x6 are equal:
(n7)⋅2n−7⋅12187=(n6)⋅2n−6⋅1729
(n7)⋅2n−7⋅729=(n6)⋅2n−6⋅2187
Dividing both sides by 2n−7:
(n7)⋅729=(n6)⋅2⋅2187
Since 2187=37, we can simplify further:
(n7)⋅729=(n6)⋅4374
Recall that:
(n7)=n!7!(n−7)!and(n6)=n!6!(n−6)!
Thus, we can express (n7) in terms of (n6):
(n7)=n−67⋅(n6)
Substitute (n7) into the equation:
n−67⋅(n6)⋅729=(n6)⋅4374
Cancel (n6) (assuming n≥6):
n−67⋅729=4374
Multiply both sides by 7:
n−6=4374⋅7729
Simplifying gives:
n−6=42⇒n=48
Thus, the value of n is 48.
Topper's Solved these Questions
- BINOMIAL THEOREM AND MATHEMATICAL INDUCTION Book:ML KHANNAChapter:BINOMIAL THEOREM AND MATHEMATICAL INDUCTION Exercise:MISCELLANEOUS EXERCISE (Matching Entries)
Explore 3 Videos
- AREA OF CURVESBook:ML KHANNAChapter:AREA OF CURVESExercise:SELF ASSESSEMENT TEST
Explore 16 Videos
- CO-ORDINATE GEOMETRY OF THREE DIMENSIONBook:ML KHANNAChapter:CO-ORDINATE GEOMETRY OF THREE DIMENSIONExercise:SELF ASSIGNMENT TEST
Explore 11 Videos
Similar Questions
Match the entries of List-A and List-B.
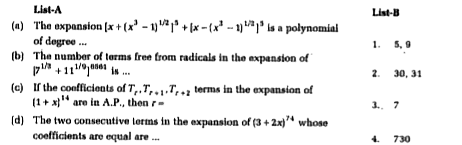
View SolutionThe value(s) of∫10x4(1−x)41+x2dx is (are)
View SolutionIf the line 2x+y=k passes through the point which divides the line segment joining the points (1,1) and (2,4) in ratio 3:2,Then k equals
View SolutionCoefficient of x^(n-2) in the product (x+1)(x+2)(x+3).........(x+n) is equal to
View SolutionIf the coefficients of x^(7) and x^(8) in the expansion of [2+(x)/(3)]^(n) are equal,then the value of n is :(A)15(B)45(C)55(D)56
View SolutionCoefficient of x6 in (1+x)(1+x2)2(1+x3)3…(1+xn)n is
View Solutionयदि (2+x3)n के प्रसार में x7 और x8 के गुणांक समान हैं , तो n का मान है -
View SolutionIf in the expansion of (1+ x )^(m) (1-x) ^(n) the coefficient of x and x ^(2) are 3 and (-6) respectively, then the value of n is-
View SolutionIn the expansion of (3+x2)n the coefficients of x7andx8 are equal, then the value of n is equal to
View SolutionThe coefficient of xn in (1−x1!+x22!−x33!+...+(−1)nxnn!)2 is equal to
View SolutionCoefficient of x3 in expansion (1+x)n is 20 then n=6 .
View SolutionCoefficient of x3 in expansion (1+x)n is 20 then n=6 .
View Solutionयदि [2+x3]n के प्रसार में x7 व x8 के गुणांक बराबर हो, तो n का मान होगा
View SolutionIf the coefficients of x7 and x8 in the expansion of (2+x3)n are equal then n =?
View Solutionif the coefficients of x7 & x8 in the expansion (2+x3)n are equal then n is equal to
View SolutionCoefficient of x6 in (1+x)(1+x2)2(1+x3)3...(1+xn)n is
View Solution
