The quartile deviation of the income of a certain person given in rupees for 12 months in a year : 129, 150,151,151,157,158,160,161,162,162,173,175
4⋅5
5⋅5
6⋅2
none of these
The correct Answer is:B
To find the quartile deviation of the income data provided, we will follow these steps:
Step 1: Organize the Data
First, we need to arrange the income data in ascending order. The given data is:
129, 150, 151, 151, 157, 158, 160, 161, 162, 162, 173, 175
The data is already sorted.
Step 2: Calculate Q1 (First Quartile)
To find the first quartile (Q1), we use the formula:
Q1=value at N+14th term
where N is the number of observations.
Here, N=12:
N+14=12+14=134=3.25
This means Q1 is located between the 3rd and 4th terms. We can calculate Q1 using interpolation:
Q1=3rd term+0.25×(4th term−3rd term)
The 3rd term is 151 and the 4th term is also 151:
Q1=151+0.25×(151−151)=151+0=151
Step 3: Calculate Q3 (Third Quartile)
Next, we calculate the third quartile (Q3) using the formula:
Q3=value at 3(N+1)4th term
Calculating:
3(N+1)4=3(12+1)4=394=9.75
This means Q3 is located between the 9th and 10th terms. We can calculate Q3 using interpolation:
Q3=9th term+0.75×(10th term−9th term)
The 9th term is 162 and the 10th term is also 162:
Q3=162+0.75×(162−162)=162+0=162
Step 4: Calculate the Quartile Deviation (QD)
Now, we can calculate the quartile deviation (QD) using the formula:
QD=Q3−Q12
Substituting the values:
QD=162−1512=112=5.5
Conclusion
The quartile deviation of the income data is 5.5.
First, we need to arrange the income data in ascending order. The given data is:
129, 150, 151, 151, 157, 158, 160, 161, 162, 162, 173, 175
To find the first quartile (Q1), we use the formula:
Q1=value at N+14th term
where N is the number of observations.
N+14=12+14=134=3.25
Q1=3rd term+0.25×(4th term−3rd term)
The 3rd term is 151 and the 4th term is also 151:
Q1=151+0.25×(151−151)=151+0=151
Next, we calculate the third quartile (Q3) using the formula:
Q3=value at 3(N+1)4th term
3(N+1)4=3(12+1)4=394=9.75
Q3=9th term+0.75×(10th term−9th term)
The 9th term is 162 and the 10th term is also 162:
Q3=162+0.75×(162−162)=162+0=162
Now, we can calculate the quartile deviation (QD) using the formula:
QD=Q3−Q12
Substituting the values:
QD=162−1512=112=5.5
The quartile deviation of the income data is 5.5.
Topper's Solved these Questions
- MEASURES OF CENTRAL TENDENCY Book:ML KHANNAChapter:MEASURES OF CENTRAL TENDENCY Exercise:Problem Set (1) (Measures of Disperation)
Explore 23 Videos
- MEASURES OF CENTRAL TENDENCY Book:ML KHANNAChapter:MEASURES OF CENTRAL TENDENCY Exercise:SELF ASSESSMENT TEST
Explore 5 Videos
- MEASURES OF CENTRAL TENDENCY Book:ML KHANNAChapter:MEASURES OF CENTRAL TENDENCY Exercise:ASSERTION / REASON
Explore 1 Video
- MAXIMA AND MINIMA Book:ML KHANNAChapter:MAXIMA AND MINIMA Exercise:MISCELANEOUS EXERCISE (COMPREHENSION)
Explore 3 Videos
- NUMERICAL METHODSBook:ML KHANNAChapter:NUMERICAL METHODSExercise:SELF ASSESSMENT TEST
Explore 10 Videos
Similar Questions
If in a series which is not highly skewed the mean deviation is 7⋅8, the approximate value of its standard deviation is
View SolutionIf the mean deviation about the median of the numbers a, 2a ,…., 50 a is 50 then |a| equals
View SolutionLet x1,x2,…..,xn be n observation and let ¯x be their arithmetic mean and σ2 be the variance
statement -1 Variance of 2x!,2x2,…,2Xn is 4σ2
Statement -2 arithmatic mean of 2x1,2x2,...,2Xn is 4¯x
View SolutionIf f:R∈R is defined by
f(x)=x2−ax+1x2+ax+1,0<a<2, the which of the following is true:
View SolutionThe first approximation to a real zero of the polynomial x3−2x−5 upto 3 decimal places by the 'false position' method is
View SolutionThe quartile deviation of daily wages (in Rs.) of 7 persons given below is 12,7,15,10,17,17,25 is
View SolutionFind out the quartile deviation and coefficient of quartile deviation of the following series:

View SolutionFind out quartile deviation and the coefficient of quartile deviation of the following series. Wages of 9 Workers in Rupees: 170,82,110,100,150,200,116,250,
View SolutionEstimate quartile deviation and the coefficient of quartile deviation of the following data: 8,9,11,12,13,17,20,21,23,25,27 Show that QD is the average of the difference between two quartiles.
View SolutionFind out quartile deviation and coefficient of quartile deviation of the following series: 28,18,20,24,30,15,47,27
View SolutionFind out quartile deviation and the coefficient of quartile deviation of the following data:
View SolutionEstimate quartile deviation and the coefficient of quartile deviation of the following series:
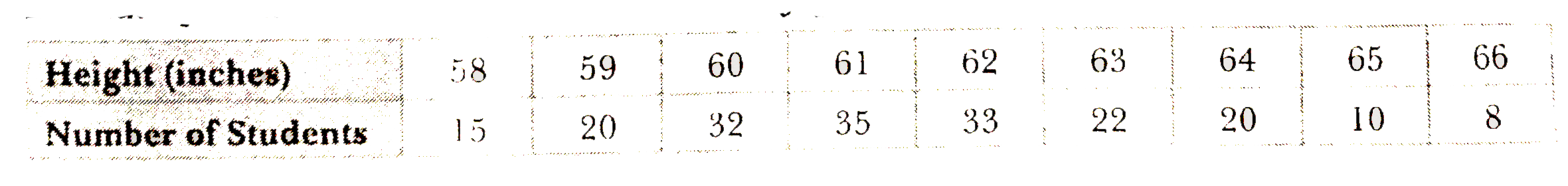
View SolutionGiven the following data, find out quartile deviation and the coefficient of quartile deviation:
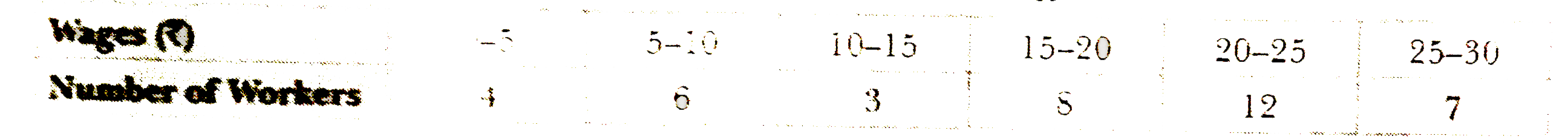
View SolutionFind out quartile deviation and coefficient of quartile deviation from the following data:
View SolutionIf the quartile deviation of a set of observations is 10 and the third quartile is 35, then the first quartile is
View SolutionThe quartile deviation of daily wages (in Rs.) of 7 persons is given below : 12, 7, 15, 10, 17,19, 25 is :
View Solution
