p⇔q is :
Tautology
Logic Equivalence
Contradiction
None of these
The correct Answer is:C
To solve the question regarding the biconditional statement p↔q, we will break down the concept and analyze the options provided. Here’s a step-by-step solution:
Step 1: Understand the Biconditional Statement
The biconditional statement p↔q (read as "p if and only if q") is true if both p and q have the same truth values. This means:
- If p is true, then q must also be true.
- If p is false, then q must also be false.
Step 2: Identify Logical Equivalence
The biconditional can be interpreted as a statement of logical equivalence. This means that p and q are logically equivalent if and only if they yield the same truth value in all possible scenarios.
Step 3: Analyze the Options
Given the options (not specified in the question), we need to identify which one correctly represents the biconditional statement p↔q. The correct option should reflect that both statements are true or both are false.
Step 4: Conclusion
Based on the understanding that p↔q indicates logical equivalence, we conclude that the correct answer is the option that states this relationship.
Final Answer
The answer is B, which represents logical equivalence.
---
The biconditional statement p↔q (read as "p if and only if q") is true if both p and q have the same truth values. This means:
- If p is true, then q must also be true.
- If p is false, then q must also be false.
The biconditional can be interpreted as a statement of logical equivalence. This means that p and q are logically equivalent if and only if they yield the same truth value in all possible scenarios.
Given the options (not specified in the question), we need to identify which one correctly represents the biconditional statement p↔q. The correct option should reflect that both statements are true or both are false.
Based on the understanding that p↔q indicates logical equivalence, we conclude that the correct answer is the option that states this relationship.
The answer is B, which represents logical equivalence.
Topper's Solved these Questions
- MATHEMATICAL REASONINGBOOK - ML KHANNACHAPTER - MATHEMATICAL REASONINGEXERCISE - PROBLEM SET (1)(FILL IN THE BLANKS)
22 Videos
- MATHEMATICAL REASONINGBOOK - ML KHANNACHAPTER - MATHEMATICAL REASONINGEXERCISE - PROBLEM SET (1)(TRUE OR FALSE)
21 Videos
- MATHEMATICAL REASONINGBOOK - ML KHANNACHAPTER - MATHEMATICAL REASONINGEXERCISE - PROBLEM SET (2) ASSERTION/REASON
3 Videos
- LOGARITHMS AND SURDSBOOK - ML KHANNACHAPTER - LOGARITHMS AND SURDSEXERCISE - Miscellaneous exercise
3 Videos
- MATRICESBOOK - ML KHANNACHAPTER - MATRICESEXERCISE - COMPREHENSION
3 Videos
Similar Questions
A declarative sentence which is either true or false is called ...... .
View SolutionWrite 'T' for True and 'F' for False.
The negation of p⇒q is p∧⌉q.
View SolutionStatement-1 : ~(p⇔~q) is equivalent to p⇔q.
Statement-2: ~(p⇔q) is a tautology
View Solution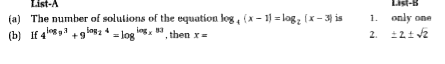

View SolutionLet p be an odd prime number and Tp be the following set of 2 x 2 matrices
Tp={A=[abca]},a,b,c∈ {0,1,2,…, p -1}
The number of A in Tp such that A is either symmetric or skew-symmetric or both and det(A) is divisible by p is: [Note: the trace of a matrix is the sum of its diagonal entries.]
View SolutionFind the truth values of
(a)(p↔~q)↔(p→p) (b)(p→q)∨~(p↔~q)
View SolutionStatements (p→q)↔(~q→~p)
View SolutionIf p and q are two propositions, then ~(p↔q) is
View Solution~[~p∧(p↔q)]≡
View SolutionThe proposition (p→q)↔(~p→~q) is a
View SolutionIf p is true and q is false then the truth values of (p↔q)↔(~q→~p) and (~p∨q)∧(~q∨p) are respectively
View SolutionThe statement (p→~q)⇔(p∧q) is a-
View Solution~(p⇒q)⇔~p∨~q is-
View SolutionStatement -1 : ~(P harr ~q) is equivalent to p harr q Statement - 2 : ~(P harr ~q) is a tautology.
View Solution~ (p rArr q) hArr ~ p vv ~ q is
View Solutionकथन - 1 : ~ (p ↔ ~ q) और p ↔ q तुल्यमान (equivalent) हैं।
कथन -2: ~ (p↔ ~q) एक पुनरुक्ति (tautology) है ।
View Solution

