Write 'T' for True and 'F' for False.
⌉(p⇒q)∨r is a dual of ⌉(p⇒q)∧r.
The correct Answer is:False
To determine whether the statement ⌉(p⇒q)∨r is a dual of ⌉(p⇒q)∧r, we will analyze both expressions step by step.
Step 1: Understand the expressions
The first expression is ⌉(p⇒q)∨r, and the second expression is ⌉(p⇒q)∧r. Here, ⌉ denotes negation, ∨ denotes disjunction (logical OR), and ∧ denotes conjunction (logical AND).
Step 2: Rewrite the implications
The implication p⇒q can be rewritten using logical operators:
- p⇒q is equivalent to ~p∨q.
Step 3: Substitute the implication
Now, substitute p⇒q in both expressions:
1. For the first expression:
- ⌉(p⇒q)∨r becomes ⌉(~p∨q)∨r.
2. For the second expression:
- ⌉(p⇒q)∧r becomes ⌉(~p∨q)∧r.
Step 4: Apply negation
Now, we need to apply the negation to both expressions:
1. The negation of ~p∨q is p∧~q (using De Morgan's laws).
2. Therefore:
- The first expression becomes p∧~q∨r.
- The second expression becomes p∧~q∧r.
Step 5: Identify the dual
According to the rules of duality:
- Disjunction (vv) is converted to conjunction (^^) and vice versa.
- Therefore, the dual of p∧~q∨r is p∧~q∧r.
Step 6: Compare the two expressions
Now we compare the two expressions:
- The first expression after transformation is p∧~q∨r.
- The dual of this expression is p∧~q∧r.
Since we see that the first expression is a disjunction and the second is a conjunction, they are not equivalent.
Conclusion
Thus, the statement ⌉(p⇒q)∨r is not a dual of ⌉(p⇒q)∧r. Therefore, the answer is F (False).
---
The first expression is ⌉(p⇒q)∨r, and the second expression is ⌉(p⇒q)∧r. Here, ⌉ denotes negation, ∨ denotes disjunction (logical OR), and ∧ denotes conjunction (logical AND).
The implication p⇒q can be rewritten using logical operators:
- p⇒q is equivalent to ~p∨q.
Now, substitute p⇒q in both expressions:
1. For the first expression:
- ⌉(p⇒q)∨r becomes ⌉(~p∨q)∨r.
2. For the second expression:
- ⌉(p⇒q)∧r becomes ⌉(~p∨q)∧r.
Now, we need to apply the negation to both expressions:
1. The negation of ~p∨q is p∧~q (using De Morgan's laws).
2. Therefore:
- The first expression becomes p∧~q∨r.
- The second expression becomes p∧~q∧r.
According to the rules of duality:
- Disjunction (vv) is converted to conjunction (^^) and vice versa.
- Therefore, the dual of p∧~q∨r is p∧~q∧r.
Now we compare the two expressions:
- The first expression after transformation is p∧~q∨r.
- The dual of this expression is p∧~q∧r.
Thus, the statement ⌉(p⇒q)∨r is not a dual of ⌉(p⇒q)∧r. Therefore, the answer is F (False).
Topper's Solved these Questions
- MATHEMATICAL REASONINGBOOK - ML KHANNACHAPTER - MATHEMATICAL REASONINGEXERCISE - PROBLEM SET (2)
15 Videos
- MATHEMATICAL REASONINGBOOK - ML KHANNACHAPTER - MATHEMATICAL REASONINGEXERCISE - PROBLEM SET (2) ASSERTION/REASON
3 Videos
- MATHEMATICAL REASONINGBOOK - ML KHANNACHAPTER - MATHEMATICAL REASONINGEXERCISE - PROBLEM SET (1)(FILL IN THE BLANKS)
22 Videos
- LOGARITHMS AND SURDSBOOK - ML KHANNACHAPTER - LOGARITHMS AND SURDSEXERCISE - Miscellaneous exercise
3 Videos
- MATRICESBOOK - ML KHANNACHAPTER - MATRICESEXERCISE - COMPREHENSION
3 Videos
Similar Questions
~(p∨q)∨(~p∧q) is logically equivalent to
View SolutionStatement-1 : ~(p⇔~q) is equivalent to p⇔q.
Statement-2: ~(p⇔q) is a tautology
View SolutionA declarative sentence which is either true or false is called ...... .
View Solution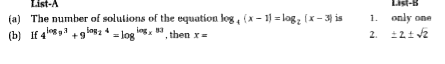

View SolutionLet p be an odd prime number and Tp be the following set of 2 x 2 matrices
Tp={A=[abca]},a,b,c∈ {0,1,2,…, p -1}
The number of A in Tp such that A is either symmetric or skew-symmetric or both and det(A) is divisible by p is: [Note: the trace of a matrix is the sum of its diagonal entries.]
View SolutionIf truth values of p, p⇒r,q⇒p are F, T, F respectively, then respective truth values of q and r
View SolutionObserve the following statements
I : The dual of [~p∧q)]∨[p∧{~(q∨~s)}] is [~(p∨q)]∧[p∨{~(q∧~s)}]
II : The dual of ~p∧[(~q)∧(p∨q)∧~r] is ~p∨[~q)∨(p∧q)∨~r]
The true statements in the above is/are :
View SolutionIf truth values of p, p implies r, q implies p are F, T, F respectively, then respective truth values of q and r
View SolutionIf p is true and q is false, then p
View SolutionWrite 'T' for True and 'F' for False.
The negation of p⇒q is p∧⌉q.
View SolutionWrite 'T' for True and 'F' for False.
p unless q means ⌉q⇒p.
View SolutionWrite 'T' for True and 'F' for False.
⌉(p⇒q)=p∧⌉q.
View SolutionWrite 'T' for True and 'F' for False. (p vv q) ^^ q = p .
View SolutionWrite 'T' for True and 'F' for False.
(p⇔q)⇔(p⇒q)∧(q⇒p).
View SolutionWrite 'T' for True and 'F' for False.
If (p∧q)⇒r in this statement '⇒' is a principal connective.
View SolutionWrite 'T' for True and 'F' for False.
If p≡q, then p⇔q will be a tautology.
View Solution

