Which of the following statement is a tautology
(~q∧p)∧q
(~q∧p)∨(p∧~p)
(~q∧p)∨(p∨~p)
(p∧q)∧(~(p∧p))
The correct Answer is:C
To determine which of the given statements is a tautology, we need to analyze each option and check if it is always true, regardless of the truth values of its components. A tautology is a statement that is true in every possible interpretation.
Let's denote the options as follows:
- Option A: ¬q∧p∧q
- Option B: ¬q∧p∨p∧¬p
- Option C: ¬q∧p∨p∨¬p
- Option D: p∨p∧q∧¬p∧p
Step 1: Analyze Option A
- The expression is ¬q∧p∧q.
- According to the Negation Law, q∧¬q is always false.
- Therefore, ¬q∧p∧q is also false for any values of p and q.
- Conclusion: Option A is not a tautology.
Step 2: Analyze Option B
- The expression is ¬q∧p∨p∧¬p.
- The term p∧¬p is always false (again by Negation Law).
- Thus, the expression simplifies to ¬q∧p.
- This expression can be true or false depending on the values of p and q.
- Conclusion: Option B is not a tautology.
Step 3: Analyze Option C
- The expression is ¬q∧p∨p∨¬p.
- The term p∨¬p is always true (by the Law of Excluded Middle).
- Thus, the entire expression simplifies to true regardless of the values of p and q.
- Conclusion: Option C is a tautology.
Step 4: Analyze Option D
- The expression is p∨p∧q∧¬p∧p.
- The term p∧¬p is always false.
- Thus, the expression simplifies to p.
- This expression can be true or false depending on the value of p.
- Conclusion: Option D is not a tautology.
Final Answer:
The only option that is a tautology is Option C: ¬q∧p∨p∨¬p.
- Option A: ¬q∧p∧q
- Option B: ¬q∧p∨p∧¬p
- Option C: ¬q∧p∨p∨¬p
- Option D: p∨p∧q∧¬p∧p
- The expression is ¬q∧p∧q.
- According to the Negation Law, q∧¬q is always false.
- Therefore, ¬q∧p∧q is also false for any values of p and q.
- Conclusion: Option A is not a tautology.
- The expression is ¬q∧p∨p∧¬p.
- The term p∧¬p is always false (again by Negation Law).
- Thus, the expression simplifies to ¬q∧p.
- This expression can be true or false depending on the values of p and q.
- Conclusion: Option B is not a tautology.
- The expression is ¬q∧p∨p∨¬p.
- The term p∨¬p is always true (by the Law of Excluded Middle).
- Thus, the entire expression simplifies to true regardless of the values of p and q.
- Conclusion: Option C is a tautology.
- The expression is p∨p∧q∧¬p∧p.
- The term p∧¬p is always false.
- Thus, the expression simplifies to p.
- This expression can be true or false depending on the value of p.
- Conclusion: Option D is not a tautology.
The only option that is a tautology is Option C: ¬q∧p∨p∨¬p.
Topper's Solved these Questions
- MATHEMATICAL REASONINGBook:ML KHANNAChapter:MATHEMATICAL REASONINGExercise:PROBLEM SET (2) ASSERTION/REASON
Explore 3 Videos
- MATHEMATICAL REASONINGBook:ML KHANNAChapter:MATHEMATICAL REASONINGExercise:PROBLEM SET (1)(TRUE OR FALSE)
Explore 21 Videos
- LOGARITHMS AND SURDSBook:ML KHANNAChapter:LOGARITHMS AND SURDSExercise:Miscellaneous exercise
Explore 3 Videos
- MATRICESBook:ML KHANNAChapter:MATRICESExercise:COMPREHENSION
Explore 3 Videos
Similar Questions
Statement-1 : ~(p⇔~q) is equivalent to p⇔q.
Statement-2: ~(p⇔q) is a tautology
View SolutionWrite 'T' for True and 'F' for False.
The negation of p⇒q is p∧⌉q.
View Solution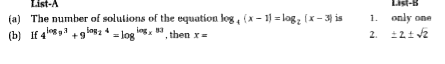

View SolutionLet p be an odd prime number and Tp be the following set of 2 x 2 matrices
Tp={A=[abca]},a,b,c∈ {0,1,2,…, p -1}
The number of A in Tp such that A is either symmetric or skew-symmetric or both and det(A) is divisible by p is: [Note: the trace of a matrix is the sum of its diagonal entries.]
View SolutionWhich one of the following statements is not a tautology ?
View SolutionWhich one of the following statement is not a tautology?
View SolutionAmong the following statements, which is a tautology ?
View SolutionWhich of the following statement pattern is a tautology?
View SolutionWhich of the following statement patternn is a tautology?
View SolutionWhich of the following statement patten is a tautology ?
View SolutionWhich of the following statement pattern is a tautology?
View SolutionWhich of the following statements is tautology ?
View SolutionWhich of the following statements is not a tautology?
View Solutionनिम्न कथनो में से कौन-सा एक, एक पुनरुक्ति (tautology) नहीं है ?
View SolutionWhich one of the following statements is a tautology ?
View SolutionWhich of the following statements is tautology ?
View Solution
