A particle is resting on a rough inclined plane with inclination α The angle of friction is λ. The particle will be at rest if and only if
α>λ
α≥λ
α≤λ
α<λ
The correct Answer is:C
To determine the conditions under which a particle remains at rest on a rough inclined plane, we need to analyze the forces acting on the particle and apply the concept of friction. Here’s a step-by-step solution:
Step 1: Identify the Forces Acting on the Particle
The forces acting on the particle on the inclined plane include:
- The gravitational force (weight) acting downwards, which can be resolved into two components:
- Perpendicular to the incline: mgcosα
- Parallel to the incline: mgsinα
- The normal force N acting perpendicular to the inclined surface.
- The frictional force Ff acting parallel to the incline, opposing the motion.
Step 2: Apply the Condition for Equilibrium
For the particle to remain at rest, the net force acting on it must be zero. This gives us two conditions:
1. The sum of forces perpendicular to the incline must be zero.
2. The sum of forces parallel to the incline must also be zero.
Step 3: Analyze the Forces Perpendicular to the Incline
The normal force N balances the perpendicular component of the weight:
N=mgcosα
Step 4: Analyze the Forces Parallel to the Incline
The frictional force Ff can be expressed in terms of the normal force and the angle of friction λ:
Ff=μN=μ(mgcosα)
Where μ=tanλ (the coefficient of friction).
For the particle to remain at rest, the frictional force must be equal to the component of the gravitational force acting down the incline:
Ff≥mgsinα
Step 5: Set Up the Inequality
Substituting the expression for Ff:
μ(mgcosα)≥mgsinα
Step 6: Simplify the Inequality
Dividing both sides by mg (assuming mg≠0):
μcosα≥sinα
Step 7: Substitute the Coefficient of Friction
Since μ=tanλ, we can substitute this into the inequality:
tanλcosα≥sinα
Step 8: Rearranging the Terms
Rearranging gives us:
cosαtanλ≥sinα
This can be rewritten as:
sinα≤tanλcosα
Step 9: Final Condition
Thus, the condition for the particle to remain at rest on the inclined plane is:
sinα≤μcosα
or equivalently,
tanα≤tanλ
Conclusion
The particle will be at rest if and only if:
α≤λ
The forces acting on the particle on the inclined plane include:
- The gravitational force (weight) acting downwards, which can be resolved into two components:
- Perpendicular to the incline: mgcosα
- Parallel to the incline: mgsinα
- The normal force N acting perpendicular to the inclined surface.
- The frictional force Ff acting parallel to the incline, opposing the motion.
For the particle to remain at rest, the net force acting on it must be zero. This gives us two conditions:
1. The sum of forces perpendicular to the incline must be zero.
2. The sum of forces parallel to the incline must also be zero.
The normal force N balances the perpendicular component of the weight:
N=mgcosα
The frictional force Ff can be expressed in terms of the normal force and the angle of friction λ:
Ff=μN=μ(mgcosα)
Where μ=tanλ (the coefficient of friction).
Ff≥mgsinα
Substituting the expression for Ff:
μ(mgcosα)≥mgsinα
Dividing both sides by mg (assuming mg≠0):
μcosα≥sinα
Since μ=tanλ, we can substitute this into the inequality:
tanλcosα≥sinα
Rearranging gives us:
cosαtanλ≥sinα
This can be rewritten as:
sinα≤tanλcosα
Thus, the condition for the particle to remain at rest on the inclined plane is:
sinα≤μcosα
or equivalently,
tanα≤tanλ
The particle will be at rest if and only if:
α≤λ
Similar Questions
Find the minimum force required to keep a block of mass m in equilibrium on a rough inclined plane with inclination α and coefficient of friction μ(<tanα).
View SolutionThe upper portion of an inclined plane of inclination α is smooth and the lower portion is rough. A particle slides down from rest from the top and just comesto rest at the foot.If the ratio ofthe smooth length to rough length is w : find the coefficient of friction.
View Solution
Knowledge Check
A particle is projected up a rough inclined plane of inclination θ and friction coefficient μ. If the time of ascent is half of the time of descent, the friction coefficient μ is equal to
A34tanθB35tanθC45tanθD12tanθA block of mass m in the equilib rium on a rough inclined plane with inclination α and coefficient of friction as shown in the figure (μ<tanα). A force F is applied on the block which makes an angle θ with the horizontal as shown in diagram.
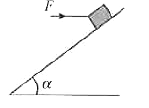 ANormal force on the block mgcosα+Fsinθ.BMinimum force f to keep the blockin equilibrium Fmin=mg(sinα−μcosα)2μ√1+μ2Cμ=tanθDNone of these
ANormal force on the block mgcosα+Fsinθ.BMinimum force f to keep the blockin equilibrium Fmin=mg(sinα−μcosα)2μ√1+μ2Cμ=tanθDNone of theseWhen a body is lying on a rough inclined plane and does not move, the force of friction
Ais equal to μRBis less than μRCis greater than μRDis equal to R
The upper portion of an incline plane of inclination α is smooth and the lower portion is rough. A particle slides down from rest from the top and just comes to rest at the fool. If the ratio of the smooth length to rough length is 2:1 and coefficient of frection is n tanα, then write the value of n.
View SolutionA particle is projected from the bottom of an inclined plane of inclination 30∘. At what angle α(from the horizontal) should the particle be projected to get the maximum range on the inclined plane.
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA block is released from rest from point on a rough inclined place of inclination 37∘. The coefficient of friction is 0.5.
View SolutionA particle of weight W rests on a rough inclined plane which makes an angle α with the horizontal . If the coefficient of static friction μ=2tanα , find the horizontal force H acting transverse to the slope of the plane when the particle is about to slip :

View Solution
