When a particle is undergoing motion, the diplacement of the particle has a magnitude that is equal to or smaller than the total distance travelled by the particle. In many cases the displacement of the particle may actually be zero, while the distance travelled by it is non-zero. Both these quantities, however depend on the frame of reference in which motion of the particle is being observed. Consider a particle which is projected in the earth's gravitational field, close to its surface, with a speed of 100√2m/s, at an angle of 45∘ with the horizontal in the eastward direction. Ignore air resistance and assume that the acceleration due to gravity is 10m/s2.
" A third observer (C) close to the surface of the reports that particle is initially travelling at a speed of 100√2m/s making on angle of 45∘ with the horizontal, but its horizontal motion is northward". The third observer is moving in :-
The south-west direction with a speed of 100√2m/s
The south-east direction with a speed of 100√2m/s
The north-west direction with a speed of 100√2m/s
The north-east direction with speed of 100√2m/s
The correct Answer is:B
To solve the problem, we need to analyze the motion of the particle and the observer's frame of reference. Let's break it down step by step:
Step 1: Understand the Initial Conditions
The particle is projected with a speed of 100√2m/s at an angle of 45∘ with the horizontal in the eastward direction. This means the initial velocity components can be calculated as follows:
- Horizontal (Eastward) component:
vox=100√2⋅cos(45∘)=100√2⋅1√2=100m/s
- Vertical component:
voy=100√2⋅sin(45∘)=100√2⋅1√2=100m/s
Step 2: Analyze the Observer's Frame of Reference
The observer (C) reports that the particle is moving with the same speed of 100√2m/s but in a northward direction. This implies that the observer must be moving in such a way that the relative motion of the particle appears northward to them.
Step 3: Determine the Observer's Velocity
To find the observer's velocity, we denote it as vc. The observer's velocity must counteract the eastward motion of the particle so that the resultant motion appears to be northward.
1. Assuming the observer moves in the southwest direction:
- If the observer moves southwest at 100√2m/s, the components of the observer's velocity would be:
vcx=−100m/s(Westward)
vcy=−100m/s(Southward)
- The relative velocity of the particle with respect to the observer would be:
vco=vox−vcx=100−(−100)=200m/s(Eastward)
- This does not result in a northward motion, so this option is incorrect.
2. Assuming the observer moves in the southeast direction:
- The components would be:
vcx=100m/s(Eastward)
vcy=−100m/s(Southward)
- The relative velocity would be:
vco=vox−vcx=100−100=0(Eastward)
- This does not yield a northward motion, so this option is incorrect.
3. Assuming the observer moves in the northwest direction:
- The components would be:
vcx=−100m/s(Westward)
vcy=100m/s(Northward)
- The relative velocity would be:
vco=vox−vcx=100−(−100)=200m/s(Eastward)
- This does not yield a northward motion, so this option is incorrect.
4. Assuming the observer moves in the northeast direction:
- The components would be:
vcx=100m/s(Eastward)
vcy=100m/s(Northward)
- The relative velocity would be:
vco=vox−vcx=100−100=0(Eastward)
- This does not yield a northward motion, so this option is incorrect.
Conclusion
From the analysis, the only viable option that allows the observer to see the particle moving northward is if the observer is moving in the southeast direction at a speed of 100√2m/s.
Final Answer
The third observer (C) is moving in the southeast direction with a speed of 100√2m/s.
The particle is projected with a speed of 100√2m/s at an angle of 45∘ with the horizontal in the eastward direction. This means the initial velocity components can be calculated as follows:
- Horizontal (Eastward) component:
vox=100√2⋅cos(45∘)=100√2⋅1√2=100m/s
- Vertical component:
voy=100√2⋅sin(45∘)=100√2⋅1√2=100m/s
The observer (C) reports that the particle is moving with the same speed of 100√2m/s but in a northward direction. This implies that the observer must be moving in such a way that the relative motion of the particle appears northward to them.
To find the observer's velocity, we denote it as vc. The observer's velocity must counteract the eastward motion of the particle so that the resultant motion appears to be northward.
- If the observer moves southwest at 100√2m/s, the components of the observer's velocity would be:
vcx=−100m/s(Westward)
vcy=−100m/s(Southward)
- The relative velocity of the particle with respect to the observer would be:
vco=vox−vcx=100−(−100)=200m/s(Eastward)
- This does not result in a northward motion, so this option is incorrect.
- The components would be:
vcx=100m/s(Eastward)
vcy=−100m/s(Southward)
- The relative velocity would be:
vco=vox−vcx=100−100=0(Eastward)
- This does not yield a northward motion, so this option is incorrect.
- The components would be:
vcx=−100m/s(Westward)
vcy=100m/s(Northward)
- The relative velocity would be:
vco=vox−vcx=100−(−100)=200m/s(Eastward)
- This does not yield a northward motion, so this option is incorrect.
- The components would be:
vcx=100m/s(Eastward)
vcy=100m/s(Northward)
- The relative velocity would be:
vco=vox−vcx=100−100=0(Eastward)
- This does not yield a northward motion, so this option is incorrect.
From the analysis, the only viable option that allows the observer to see the particle moving northward is if the observer is moving in the southeast direction at a speed of 100√2m/s.
The third observer (C) is moving in the southeast direction with a speed of 100√2m/s.
Topper's Solved these Questions
- KINEMATICSBOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Comprehension#7
1 Video
- KINEMATICSBOOK - ALLENCHAPTER - KINEMATICSEXERCISE - EXERCISE-04[A]
35 Videos
- KINEMATICSBOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Comprehension#5
6 Videos
- ERROR AND MEASUREMENTBOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
Similar Questions
A projectile is projected with some initial velocity and some initial angle of projection. A wind is also blowing, due to which constant horizontal retardation a is imparted to the particle in the plane of motion. It is found that, the particle is at same height at two different time t1 & t2 and particle is at same horizontal distance at two different time t3 & t4
Angle of projection of particle is :-
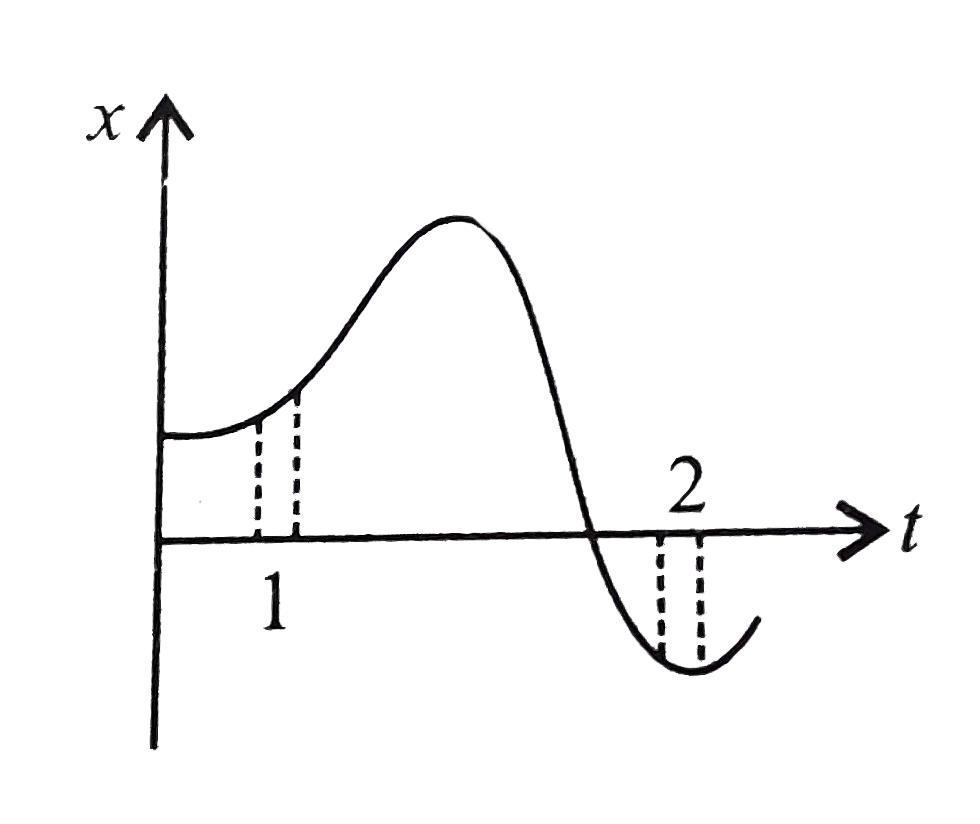
View SolutionFigure shows the x-t plot of a particle in one-dimensional motion. Two different equal intervals of time are shown. Let ν1 and ν2 be average speed in time intervals 1 and 2 respectively. Then
View SolutionA circus wishes to develop a new clown act. Fig. (1) shows a diagram of the proposed setup. A clown will be shot out of a cannot with velocity v0 at a trajectory that makes an angle θ=45∘ with the ground. At this angile, the clown will travell a maximum horizontal distance. The cannot will accelerate the clown by applying a constant force of 10,000N over a very short time of 0.24s. The height above the ground at which the clown begins his trajectory is 10m.

A large hoop is to be suspended from the celling by a massless cable at just the right place so that the clown will be able to dive through it when he reaches a maximum height above the ground. After passing through the hoop he will then continue on his trajectory until arriving at the safety net. Fig (2) shows a graph of the vertical component of the clown's velocity as a function of time between the cannon and the hoop. Since the velocity depends on the mass of the particular clown performing the act, the graph shows data for serveral different masses.

If the angle the cannot makes with the horiaontal is increased from 45∘, the hoop will have to be
View SolutionA cube has a side of length 1.2×10−2m. Its volume upto correct significant figures is
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travel in a vertical plane, calculate
the time for which the ball is in the air. (g=10 m/s2)
View SolutionWhen a particle is undergoing motion, the diplacement of the particle has a magnitude that is equal to or smaller than the total distance travelled by the particle. In many cases the displacement of the particle may actually be zero, while the distance travelled by it is non-zero. Both these quantities, however depend on the frame of reference in which motion of the particle is being observed. Consider a particle which is projected in the earth's gravitational field, close to its surface, with a speed of 100√2m/s, at an angle of 45∘ with the horizontal in the eastward direction. Ignore air resistance and assume that the acceleration due to gravity is 10m/s2.
The motion of the particle is observed in two different frames: one in the ground frame (A) and another frame (B), in which the horizontal component of the displacement is always zero. Two observers locates in these frames ill agree on :-
View SolutionWhen a particle is undergoing motion, the diplacement of the particle has a magnitude that is equal to or smaller than the total distance travelled by the particle. In many cases the displacement of the particle may actually be zero, while the distance travelled by it is non-zero. Both these quantities, however depend on the frame of reference in which motion of the particle is being observed. Consider a particle which is projected in the earth's gravitational field, close to its surface, with a speed of 100sqrt(2) m//s , at an angle of 45^(@) with the horizontal in the eastward direction. Ignore air resistance and assume that the acceleration due to gravity is 10 m//s^(2) . There exists a frame (D) in which the distance travelled by the particle is minimum. This minimum distance is equal to :-
View SolutionWhen a particle is undergoing motion, the diplacement of the particle has a magnitude that is equal to or smaller than the total distance travelled by the particle. In many cases the displacement of the particle may actually be zero, while the distance travelled by it is non-zero. Both these quantities, however depend on the frame of reference in which motion of the particle is being observed. Consider a particle which is projected in the earth's gravitational field, close to its surface, with a speed of 100√2m/s, at an angle of 45∘ with the horizontal in the eastward direction. Ignore air resistance and assume that the acceleration due to gravity is 10m/s2.
Consider an observer in frame D (of the previous question), who observes a body of mass 10 kg acelerating in the upward direction at 30m/s2 (w.r.t. himself). The net force acting on this body, as observed from the ground is :-
View SolutionSTATEMENT - 1 : Distance travelled by a particle moving rectilinearly may not be equal to magnitude of displacement of the particle. and STATEMENT - 2 : Distance travelled is a scalar but displacement is a vector.
View SolutionThe equation for the motion of a particle is v = at . The distance travelled by the particle in the first 4 second is :
View SolutionThe motion of a particle is described by the equation v = at. The distance travelled by the particle in the first 4s
View SolutionIf distance travelled by particle is zero then its displacement is …... .
View Solutionयदि किसी कण का विस्थापन शून्य है तो तय की गयी दूरी :
View SolutionThe actual distance travelled by the particle during its motion is called ______
View SolutionThe actual distance travelled by the particle during its motion is called
View SolutionSTATEMENT - 1 : Distance travelled by a particle moving rectilinearly may not be equal to magnitude of displacement of the particle. and STATEMENT - 2 : Distance travelled is a scalar but displacement is a vector.
View Solution

