Two moles of an ideal monoatomic gas, initially at pressure p1 and volume V1, undergo an adiabatic compression until its volume is V2. Then the gas is given heat Q at constant volume V2.
(i) Sketch the complete process on a p-V diagram.
(ii) Find the total work done by the gas, the total change in its internal energy and the final temperature of the gas. [Give your answer in terms of p1,V1,V2,QandR]
The correct Answer is:(i) (##ALNPHYC07(I)E01440_A01##) (ii) W=32P1V1[1−(V1V2)2/3],ΔU=32P1V1[(V1V2)2/3−1],T=Q3R+P1V22R(V1V2)2/3
To solve the problem step-by-step, we will break it down into parts as follows:
Part (i): Sketch the complete process on a p-V diagram
1. Identify the Initial State: The initial state of the gas is given by pressure p1 and volume V1. Plot this point on the p-V diagram.
2. Adiabatic Compression: The gas undergoes adiabatic compression from volume V1 to V2. This process is represented by a curve on the p-V diagram, moving from point 1 (at V1,p1) to point 2 (at V2,p2). The pressure increases as the volume decreases.
3. Constant Volume Heating: After reaching volume V2, the gas is heated at constant volume V2. This process is represented by a vertical line moving from point 2 (at V2,p2) to point 3 (at V2,p3), where p3 is the new pressure after heat Q is added.
4. Label the Diagram: Clearly label the points as follows:
- Point 1: (V1,p1)
- Point 2: (V2,p2)
- Point 3: (V2,p3)
Part (ii): Find the total work done by the gas, the total change in its internal energy, and the final temperature of the gas.
Step 1: Total Work Done by the Gas
1. Work Done during Adiabatic Compression (1 to 2):
The work done during an adiabatic process is given by:
W1→2=p1V1−p2V2γ−1
where γ=CpCv=53 for a monoatomic gas.
2. Finding p2:
Using the adiabatic condition:
p1Vγ1=p2Vγ2
Rearranging gives:
p2=p1(V1V2)γ
3. Substituting p2 into Work Done:
Substitute p2 into the work done equation:
W1→2=p1V1−p1(V1V2)γV2γ−1
Simplifying gives:
W1→2=p1V1γ−1(1−(V1V2)γ−1)
4. Work Done during Constant Volume Process (2 to 3):
Since the volume is constant, the work done W2→3=0.
5. Total Work Done:
Wtotal=W1→2+W2→3=W1→2
Step 2: Total Change in Internal Energy
1. Change in Internal Energy for Process 1 to 2:
The change in internal energy during an adiabatic process is given by:
ΔU1→2=nCv(T2−T1)
For a monoatomic gas, Cv=32R.
2. Change in Internal Energy for Process 2 to 3:
For the constant volume process, the change in internal energy is equal to the heat added:
ΔU2→3=Q
3. Total Change in Internal Energy:
ΔUtotal=ΔU1→2+ΔU2→3=nCv(T2−T1)+Q
Step 3: Final Temperature of the Gas
1. Using the Ideal Gas Law:
The final temperature can be found using the ideal gas law:
pV=nRT
For state 1:
T1=p1V1nR
For state 2:
T2=p2V2nR
For state 3:
T3=p3V2nR
2. Relate T3 to Q:
Using the relation for change in internal energy and the heat added, we can express T3 in terms of Q:
ΔUtotal=nCv(T3−T1)=Q
3. Final Expression for T3:
Rearranging gives:
T3=T1+QnCv
Final Answers
- Total Work Done:
Wtotal=p1V1γ−1(1−(V1V2)γ−1)
- Total Change in Internal Energy:
ΔUtotal=nCv(T2−T1)+Q
- Final Temperature:
T3=T1+QnCv
- Point 1: (V1,p1)
- Point 2: (V2,p2)
- Point 3: (V2,p3)
The work done during an adiabatic process is given by:
W1→2=p1V1−p2V2γ−1
where γ=CpCv=53 for a monoatomic gas.
Using the adiabatic condition:
p1Vγ1=p2Vγ2
Rearranging gives:
p2=p1(V1V2)γ
Substitute p2 into the work done equation:
W1→2=p1V1−p1(V1V2)γV2γ−1
Simplifying gives:
W1→2=p1V1γ−1(1−(V1V2)γ−1)
Since the volume is constant, the work done W2→3=0.
Wtotal=W1→2+W2→3=W1→2
The change in internal energy during an adiabatic process is given by:
ΔU1→2=nCv(T2−T1)
For a monoatomic gas, Cv=32R.
For the constant volume process, the change in internal energy is equal to the heat added:
ΔU2→3=Q
ΔUtotal=ΔU1→2+ΔU2→3=nCv(T2−T1)+Q
The final temperature can be found using the ideal gas law:
pV=nRT
For state 1:
T1=p1V1nR
For state 2:
T2=p2V2nR
For state 3:
T3=p3V2nR
Using the relation for change in internal energy and the heat added, we can express T3 in terms of Q:
ΔUtotal=nCv(T3−T1)=Q
Rearranging gives:
T3=T1+QnCv
Wtotal=p1V1γ−1(1−(V1V2)γ−1)
ΔUtotal=nCv(T2−T1)+Q
T3=T1+QnCv
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE - 05 (B) (MCQ)
Explore 9 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE - 05 (B) (MATCH THE COLUMN)
Explore 3 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE - 05 (A)
Explore 73 Videos
- CURRENT ELECTRICITYBook:ALLENChapter:CURRENT ELECTRICITYExercise:EX.II
Explore 66 Videos
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:EXERCISE 4
Explore 9 Videos
Similar Questions
Two moles of an ideal monoatomic gas, initially at pressure p1 and volume V1, undergo an adiabatic compression until its volume is V2. Then the gas is given heat Q at constant volume V2.
(i) Sketch the complete process on a p-V diagram.
(ii) Find the total work done by the gas, the total change in its internal energy and the final temperature of the gas. [Give your answer in terms of p1,V1,V2,QandR]
View SolutionA monoatomic gas at a pressure p, having a volume 2V and then adiabatically to a volume 16 V. The final pressure of the gas is (take γ=53 )
View Solution
Knowledge Check
Two moles of an ideal monoatomic gas occupy a volume 2V at temperature 300K, it expands to a volume 4V adiabatically, then the final temperature of gas is
Aa.179 KBb.189 KCc.199 KDd.219 KAn ideal gas undergoes cyclic process ABCDA as shown in given p−V diagram. The amount of work done by the gas is
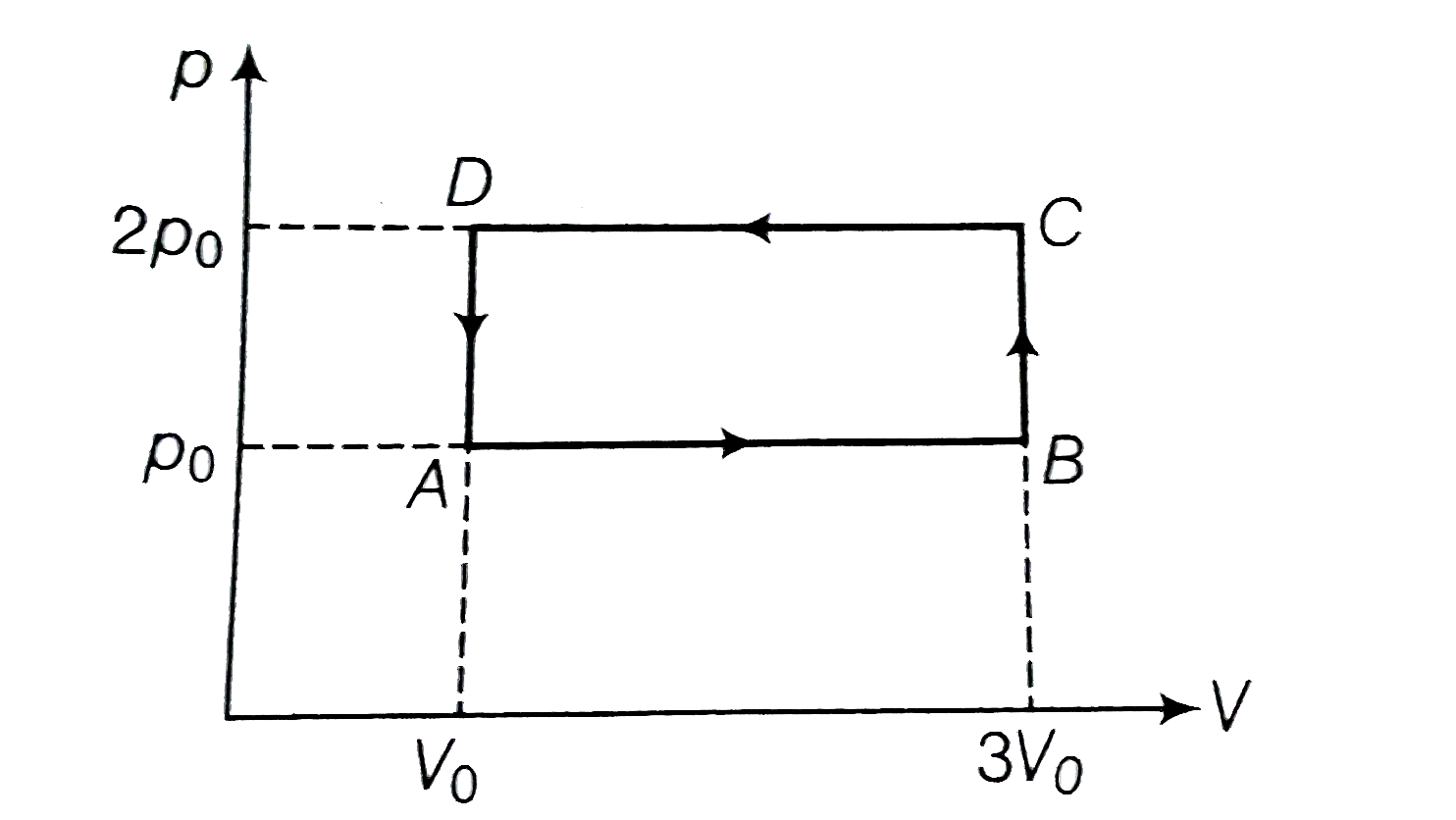 A6P0V0B−2P0V0C+2P0V0D+4P0V0
A6P0V0B−2P0V0C+2P0V0D+4P0V0
A monoatomic gas at pressure P1 and volume V1 is compressed adiabatically to 18th of its original volume. What is the final pressure of gas.
View SolutionThree moles of an ideal gas (Cp=72R) at pressure p0 and temperature T0 is isothermally expanded to twice its initial volume. It is then compressed at a constant pressure to its original volume.
(a) Sketch p-V and p-T diagram for complete process.
(b) Calculate net work done by the gas.
(c) Calculate net heat supplied to the gas during complete process.
(Write your answer in terms of gas constant =R)
View SolutionThere are two parts of a vessel. The pressure in one part is P and its volume is V. the volume of another part is 4V and there is vaccum in it. If the intervening wall is ruptured, then work done by the gas and change in its internal energy will be

View SolutionTwo moles of an ideal monatomic gas occupies a volume V at 27 °C. The gas expands adiabatically to a volume 2V. Calculate (i) the final temperature of the gas and (ii) change in its internal energy.
View SolutionTwo moles of helium gas(λ=5/3) are initially at temperature 27∘C and occupy a volume of 20 litres. The gas is first expanded at constant pressure until the volume is doubled. Then it undergoes an adiabatic change until the temperature returns to its initial value.
(i) Sketch the process on a p-V diagram.
(ii) What are the final volume and pressure of the gas?
(iii) What is the work done by the gas ?
View SolutionTwo moles of helium gas(λ=5/3) are initially at temperature 27∘C and occupy a volume of 20 litres. The gas is first expanded at constant pressure until the volume is doubled. Then it undergoes an adiabatic change until the temperature returns to its initial value.
(i) Sketch the process on a p-V diagram.
(ii) What are the final volume and pressure of the gas?
(iii) What is the work done by the gas ?
View Solution
