In the string mass system shown in the figure, the string is compressed by x0=mg2k from its natural length and block is relased from rest. Find the speed o the block when it passes through P (mg/4k distance from mean position)
_S01_030_Q01.png)
ω=√3km,x=Asin(ωt+ϕ),v=Aωcos(ωt+ϕ) at t=0,x=0⇒ϕ=0
x=Asinωt⇒mg4k=mg2ksinωt⇒sinωt=12⇒ωt=π6⇒t=π6ω=T12
v=Aωcosωt.V=mg2k√3kmcos[√3km(2π√m3k/12)]=g√9m16k
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:SOME WORKED OUT EXAMPLES
Explore 29 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise-01
Explore 117 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 24 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
Similar Questions
A simple pendulum has time period 2s. The point of suspension is now moved upward accoding to relation y=(6t−3.75t2)m where t is in second and y is the vertical displacement in upward direction. The new time period of simple pendulum will be
View SolutionThe equation of motion of a particle of mass 1g is d2xdt2+π2x=0, where x is displacement (in m) from mean position. The frequency of oscillation is (in Hz)
View SolutionThe freqency of a radar is 780 M hz. The frequency of the reflected wave from an aerolane is increased by 2.6 kHz. The velocity of aeroplane is
View SolutionChoose the correct statement:
View SolutionA wheel of moment of inertia I and rdius r is free to rotate about its centre as shown in figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. Find the speed of the block as it descends through a height h.

View SolutionThe system shown in figure is released is released from rest . Find acceleration of different string blocks and tenson in different strings.
View SolutionA block of mass m is released from rest onto a spring. A having stiffness kA=mg/2h as shown in figure. If the block compresses spring B through a distance h, find the:

a. stiffness of the spring B
b. equilibrium position of the block
c. maximum velocity of the block
d. maximum acceleration of the block
View SolutionBlock A of the mass M in the figure is released from rest when the extension in the spring is x0. The maximum downwards displacement of the block is (assume x0<Mg/k).
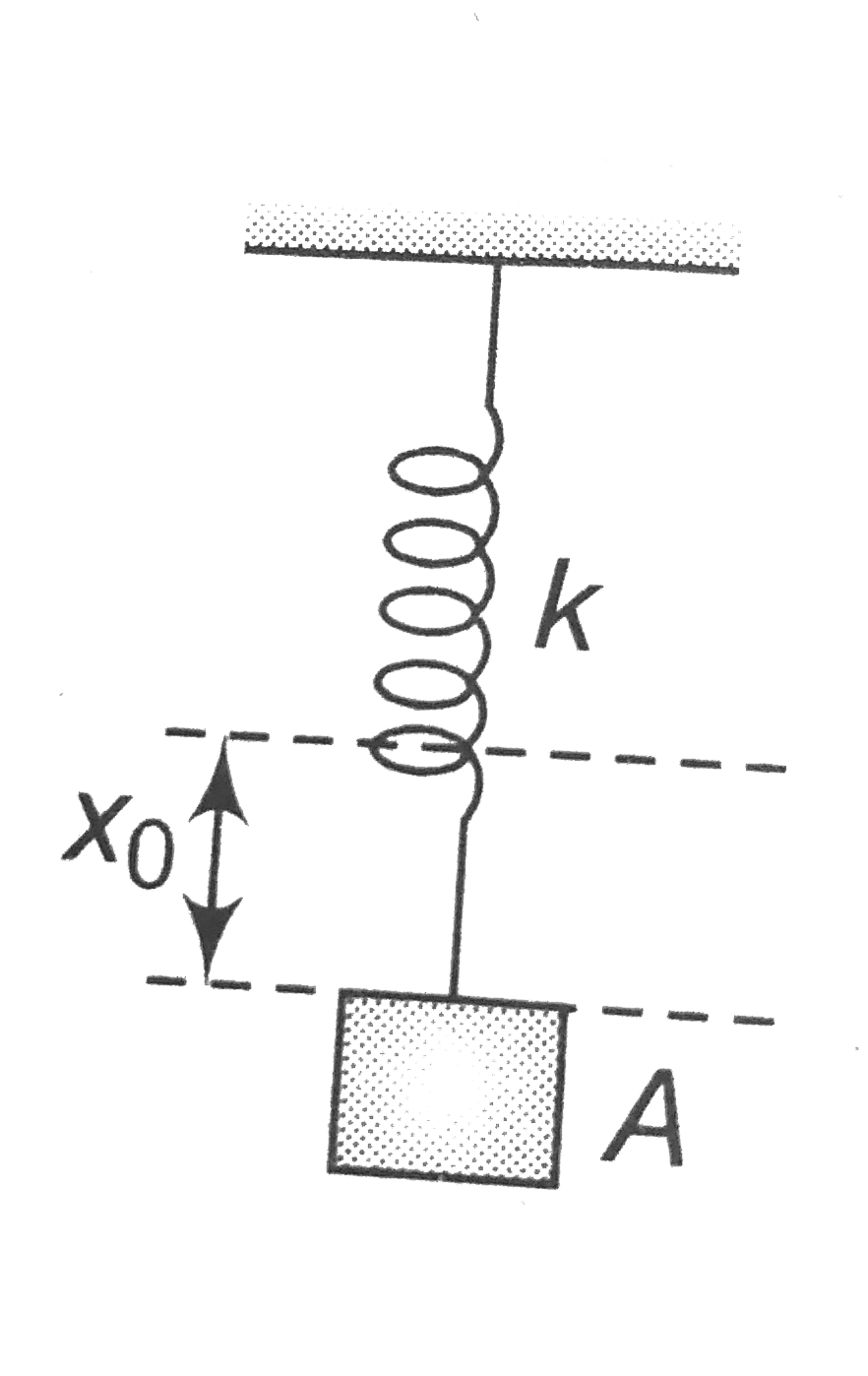
View SolutionBlock A in the figure is released from rest when the extension in the spring is x0(x0<mg/k). The maximum downward displacement of the block is (there is no friction) :

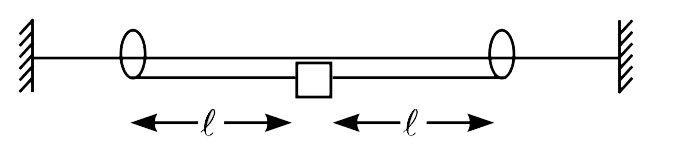
View SolutionTwo small rings each of mass ‘m’ are connected to a block of same mass ‘m’ through inextensible light strings. Rings are constrained to move along a smooth horizontal rod. Initially system is held at rest (as shown in figure) with the strings just taut. Length of each string is ‘l’. The system is released from the position shown. Find the speed of the block (v) and speed of the rings (u) when the strings make an angle of theta=60^(@)withvertical.(Takeg = 10 m//s^2)
View SolutionIn the shown mass pulley system, pulleys and string are massless. The one end of the string is pulled by the force F = mg. The acceleration of the block will be :

View SolutionA block of mass m is hung vertically from an elastic thread of force constant mg/a. Initially the thread was at its natural length and the block is allowed to fall freely. Kinetic energy of the block when it passes through the equilibrium position will be
View SolutionIn the given figure, Find mass of the block A, if it remains at rest, when the system is released from rest. Pulleys and strings are massless. [g=10m/s2]

View SolutionThe block shown in figure is released from rest. Find out the speed of the block when the spring is compressed by 1 m
View SolutionIn the system shown in figure, the block A is released from rest. Find
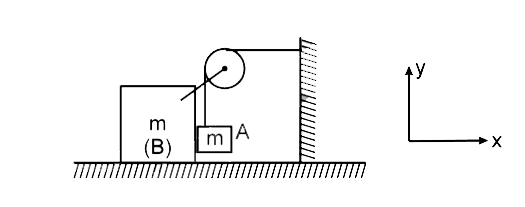
Tension in the string.
View SolutionThe system shown in figure is released is released from rest . Find acceleration of different string blocks and tenson in different strings.
View Solution
