Ifx2+y2=4anda2+b2=9 then
maximum value of (abxy)is 9
maximum value of (abxy)is 36
maximum value of (ax+by) is 6
minimum value of (ax+by) is -6
The correct Answer is:A, C, D
To solve the problem given, we need to analyze the equations provided and find the number of integer solutions for the equations x2+y2=4 and a2+b2=9.
Step 1: Solve the first equation x2+y2=4
We can find integer pairs (x,y) that satisfy this equation. The possible integer values for x and y can be derived from the equation:
1. x=0:
- y2=4⇒y=±2
- Solutions: (0,2), (0,−2)
2. x=1:
- 12+y2=4⇒y2=3 (not an integer)
3. x=2:
- 22+y2=4⇒y2=0⇒y=0
- Solution: (2,0)
4. x=−1:
- (−1)2+y2=4⇒y2=3 (not an integer)
5. x=−2:
- (−2)2+y2=4⇒y2=0⇒y=0
- Solution: (−2,0)
Thus, the integer solutions for x2+y2=4 are:
- (0,2)
- (0,−2)
- (2,0)
- (−2,0)
Total solutions: 4 pairs.
Step 2: Solve the second equation a2+b2=9
Similarly, we find integer pairs (a,b) that satisfy this equation:
1. a=0:
- b2=9⇒b=±3
- Solutions: (0,3), (0,−3)
2. a=1:
- 12+b2=9⇒b2=8 (not an integer)
3. a=2:
- 22+b2=9⇒b2=5 (not an integer)
4. a=3:
- 32+b2=9⇒b2=0⇒b=0
- Solution: (3,0)
5. a=−1:
- (−1)2+b2=9⇒b2=8 (not an integer)
6. a=−2:
- (−2)2+b2=9⇒b2=5 (not an integer)
7. a=−3:
- (−3)2+b2=9⇒b2=0⇒b=0
- Solution: (−3,0)
Thus, the integer solutions for a2+b2=9 are:
- (0,3)
- (0,−3)
- (3,0)
- (−3,0)
Total solutions: 4 pairs.
Step 3: Combine the solutions
Now, we can combine the solutions from both equations. Each pair from the first equation can be combined with each pair from the second equation.
Total combinations = (Number of solutions for x2+y2=4) × (Number of solutions for a2+b2=9) = 4×4=16.
Final Answer
Thus, the total number of integer solutions for the given equations is 16.
- y2=4⇒y=±2
- Solutions: (0,2), (0,−2)
- 12+y2=4⇒y2=3 (not an integer)
- 22+y2=4⇒y2=0⇒y=0
- Solution: (2,0)
- (−1)2+y2=4⇒y2=3 (not an integer)
- (−2)2+y2=4⇒y2=0⇒y=0
- Solution: (−2,0)
- (0,2)
- (0,−2)
- (2,0)
- (−2,0)
- b2=9⇒b=±3
- Solutions: (0,3), (0,−3)
- 12+b2=9⇒b2=8 (not an integer)
- 22+b2=9⇒b2=5 (not an integer)
- 32+b2=9⇒b2=0⇒b=0
- Solution: (3,0)
- (−1)2+b2=9⇒b2=8 (not an integer)
- (−2)2+b2=9⇒b2=5 (not an integer)
- (−3)2+b2=9⇒b2=0⇒b=0
- Solution: (−3,0)
- (0,3)
- (0,−3)
- (3,0)
- (−3,0)
Topper's Solved these Questions
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:MATHEMATICS
Explore 25 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS SECTION-I
Explore 2 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:Chemistry
Explore 54 Videos
- SEQUENCE AND PROGRESSIONBook:ALLENChapter:SEQUENCE AND PROGRESSIONExercise:Exercise (JA)
Explore 12 Videos
- TEST PAPERSBook:ALLENChapter:TEST PAPERSExercise:PHYSICS
Explore 4 Videos
Similar Questions
5∑k=01sin[(K+1)θ]sin[(K+2)θ] can be equal to
View SolutionIf →A=3ˆi+4ˆj and →B=6ˆi+8ˆj, select correct alternatives :- (i)→A.→B=50 (ii)2A=B (iii)ˆA=ˆB (iv)ˆA×→B=→0
View SolutionTangents PA and PB are drawn to the circle x2+y2=8 from any arbitrary point P on the line x+y=4. The locus of the mid-point of chord of contact AB is
View SolutionIf the sum of first n terms of an A.P. is cn2 then the sum of squares of these n terms is
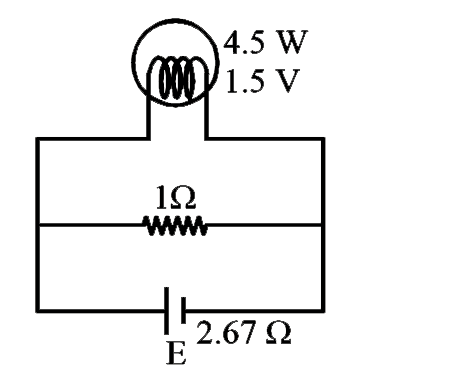
View SolutionAtorch bulb rated is 4.5W1.5V is connected as shwon in the figure. The emc (in V) of the cell needed to make the bulb glow at full intensity is:
View SolutionR={x,y):x,y in R,x^(2)+y^(2) =((4)/(9))x^(2)} then
View SolutionLocus of feet of perpendicular from (5,0) to the tangents of (x^(2))/(16)-(y^(2))/(9)=1 is (A)x^(2)+y^(2)=4(B)x^(2)+y^(2)=16(C)x^(2)+y^(2)=9(D)x^(2)+y^(2)=25
View SolutionSuppose x,y in(-2,2) and xy=-1 then the minimum value of a=(4)/(4-x^(2))-(9)/(9-y^(2)) is
View SolutionFactorize each of the following expressions:
(1)x4−625
(2) x4−1
(3)49(a−b)2−25(a+b)2
(4) x−y−x2+y2
View SolutionIf 22+22+2x=3 , then x is equal to −47 (b) 47 (c) −49 (d) 49
View Solutionगुणनखंड ज्ञात कीजिये-
9(x+y)2−12(x2−y2)+4(x−y)2
View Solutionदीर्घवृत्त x29+y24=1 तथा x24+y29=1 की उत्केंद्रताएँ असमान है।
View SolutionThe number of common tangents to x2+y2=4,(x−3)2+(y−4)2=9 is
View SolutionTangents are drawn from points on the hyperbola x29−y24=1 to the circle x2+y2=9. Then show that the locus of the mid point of the chord of contact is (x2+y2)2=81(x29−y24)
View Solutionयदि A=[(x,y):x2+y2=25] तथा B=[(x,y):x2+9y2=144] , तब A∩B में है / है
View SolutionFor which of the hyperbolas, can we have more than one pair of perpendicular tangents? (a)x24−y29=1 (b) x24−y29=−1 (c)x2−y2=4 (d) xy=44
View Solution
