Depending on in which quadrant an angle θ lies, functions cosθ and sinθ may be positive or negative. In the second column of the given lable are specified whether these functions are positive or negative and in the first column are specified quadrants.
Column-IColumn-II(A) First(P)sinθ is positive(B) Second(Q)sinθ is negative(C) Third(R)cosθ is negative(D) Fourth(S)tanθ and sinθboth are negative(T)secθ is negative and sinθ is positive
The correct Answer is:(A)→(P);(B)→(P,R,T);(C)→(Q,R);(D)→(Q,S)
To solve the problem, we need to determine the signs of the trigonometric functions sinθ, cosθ, and tanθ in each of the four quadrants and match them with the given options in Column II.
Step 1: Analyze the First Quadrant
In the First Quadrant (0° to 90°):
- sinθ is positive
- cosθ is positive
- tanθ is positive
Matching:
- sinθ is positive (P) → Matches with A.
Step 2: Analyze the Second Quadrant
In the Second Quadrant (90° to 180°):
- sinθ is positive
- cosθ is negative
- tanθ is negative
Matching:
- sinθ is positive (P) → Matches with B.
- cosθ is negative (R) → Matches with B.
- secθ is negative and sinθ is positive (T) → Matches with B.
Step 3: Analyze the Third Quadrant
In the Third Quadrant (180° to 270°):
- sinθ is negative
- cosθ is negative
- tanθ is positive
Matching:
- sinθ is negative (Q) → Matches with C.
- cosθ is negative (R) → Matches with C.
- tanθ is positive, so tanθ and sinθ both are negative (S) → Does not match.
Step 4: Analyze the Fourth Quadrant
In the Fourth Quadrant (270° to 360°):
- sinθ is negative
- cosθ is positive
- tanθ is negative
Matching:
- sinθ is negative (Q) → Matches with D.
- tanθ and sinθ both are negative (S) → Matches with D.
- secθ is positive, so it does not match.
Final Matching:
- A → P (First Quadrant)
- B → P, R, T (Second Quadrant)
- C → Q, R (Third Quadrant)
- D → Q, S (Fourth Quadrant)
Summary of Matches:
- A → P
- B → P, R, T
- C → Q, R
- D → Q, S
In the First Quadrant (0° to 90°):
- sinθ is positive
- cosθ is positive
- tanθ is positive
- sinθ is positive (P) → Matches with A.
In the Second Quadrant (90° to 180°):
- sinθ is positive
- cosθ is negative
- tanθ is negative
- sinθ is positive (P) → Matches with B.
- cosθ is negative (R) → Matches with B.
- secθ is negative and sinθ is positive (T) → Matches with B.
In the Third Quadrant (180° to 270°):
- sinθ is negative
- cosθ is negative
- tanθ is positive
- sinθ is negative (Q) → Matches with C.
- cosθ is negative (R) → Matches with C.
- tanθ is positive, so tanθ and sinθ both are negative (S) → Does not match.
In the Fourth Quadrant (270° to 360°):
- sinθ is negative
- cosθ is positive
- tanθ is negative
- sinθ is negative (Q) → Matches with D.
- tanθ and sinθ both are negative (S) → Matches with D.
- secθ is positive, so it does not match.
- A → P (First Quadrant)
- B → P, R, T (Second Quadrant)
- C → Q, R (Third Quadrant)
- D → Q, S (Fourth Quadrant)
- A → P
- B → P, R, T
- C → Q, R
- D → Q, S
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Differentiation)
38 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Integration)
12 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - PHYSICS
13 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Video
Similar Questions
For a straight line y=43x−4. Choose correct alternate(s)
View SolutionFind the value of x1, so that ∫x10ydx=5
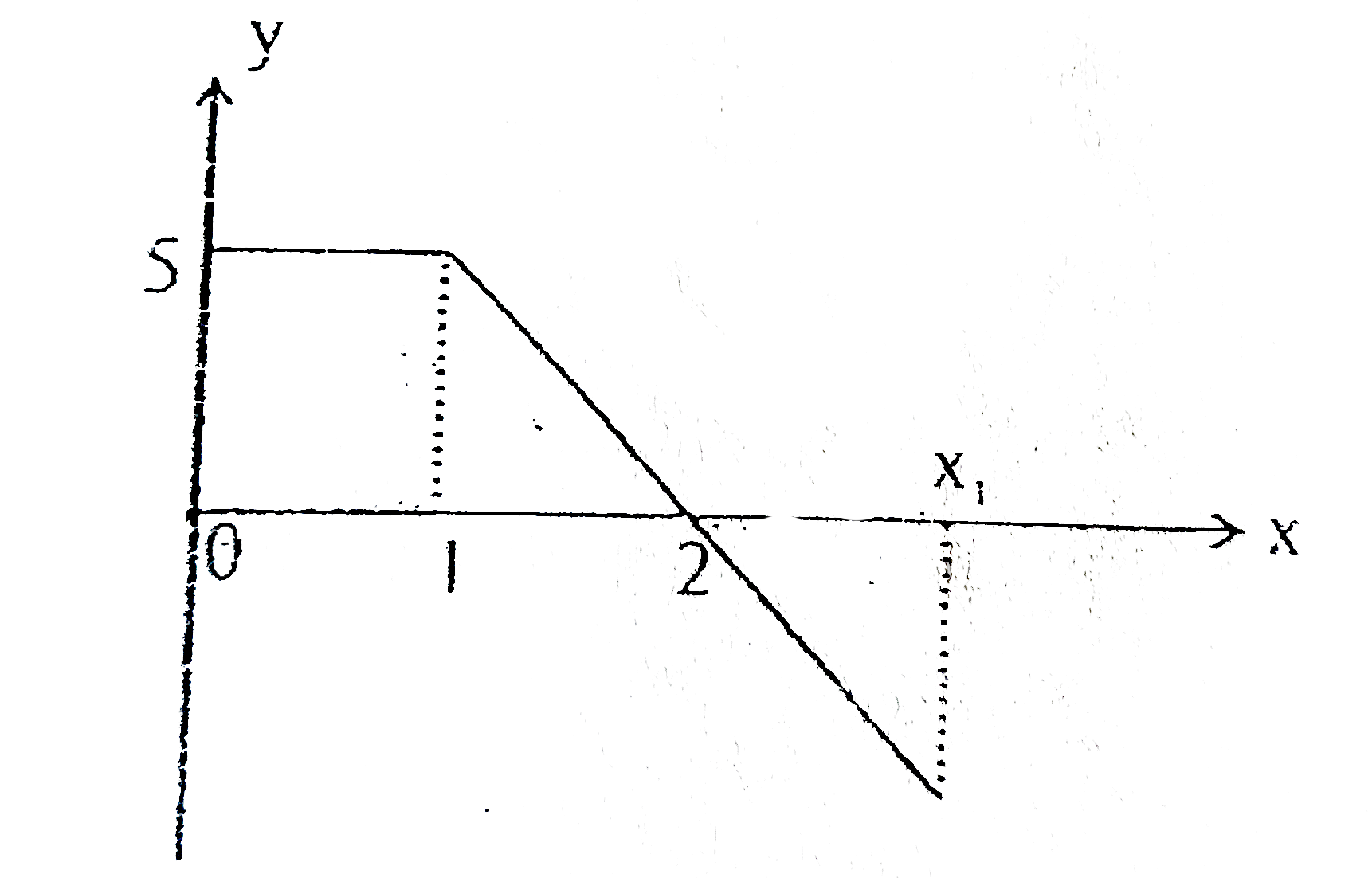
View SolutionThe graph shown the extension of is wire of length 1 m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross sectional area of the wire is 1mm2, then the Young's modulus of the material of the wire.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_RACE_R64_E01_001_Q01.png" width="80%"gt
View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.
View SolutionA disc is made to oscillate about a horizontal axis passing through one of its ends and its behaves like a second's pendulum. Determine its lengths.
View SolutionIf theta lies in the second quadrant, then the value sqrt(((1-sintheta)/(1+sintheta)))+sqrt(((1+sintheta)/(1-sintheta)))
View SolutionIf tantheta=(24)/(7) and sintheta is negative then value of costheta will be
View SolutionLet X={θ∈[0,2π]:sinθ=cosθ}
Assertion (A) : The number of elements in X is 2.
Reason ( R ) : sinθandcosθ are both negative both in second and fourth quadrants.
View Solutioncosθ⋅cscθ−sinθ⋅secθcosθ+sinθ
View Solutioncosθ[cosθsinθ−sinθcosθ]+sinθ[sinθ−cosθcosθsinθ]=
View SolutionIf cosθ=−34andtanθ is negative, the value of sinθ is
View SolutionIf sinθ=2425 and θ lies in II quadrant, then secθ+tanθ=...........
View SolutionIf sinθ=2425 and θ lies in II quadrant, then secθ+tanθ= _________
View SolutionFind the quadrant in which θ lies if
(i)cos θ is negative but sin θ is positive
(ii)sin θ is negative but tan θ is positive
(iii) cos θ is negative and sin θ is negative
(iv) cos θ and cot θ are both negative
(v) sec θ is positive but cosec θ is negative
View SolutionIf tanθ=3 and θ lies in third quadrant then sinθ=
View SolutionIf sinθ+cosθ=0andθ lies in the fourth quadrant, find sinθandcosθ
View Solution

