A particle moves along with X-axis. The position x of particle with respect to time t from given by x=b0+b1t+b2t2. The acceleration of particle is
a1
a2
2a2
3a2
The correct Answer is:C
Step by step video solution for A particle moves along with X-axis. The position x of particle with respect to time t from given by x=b_(0)+b_(1)t+b_(2)t^(2). The acceleration of particle is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Integration)
12 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Graphs))
29 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Trigonometry)
22 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Video
Similar Questions
Find the value of x1, so that ∫x10ydx=5
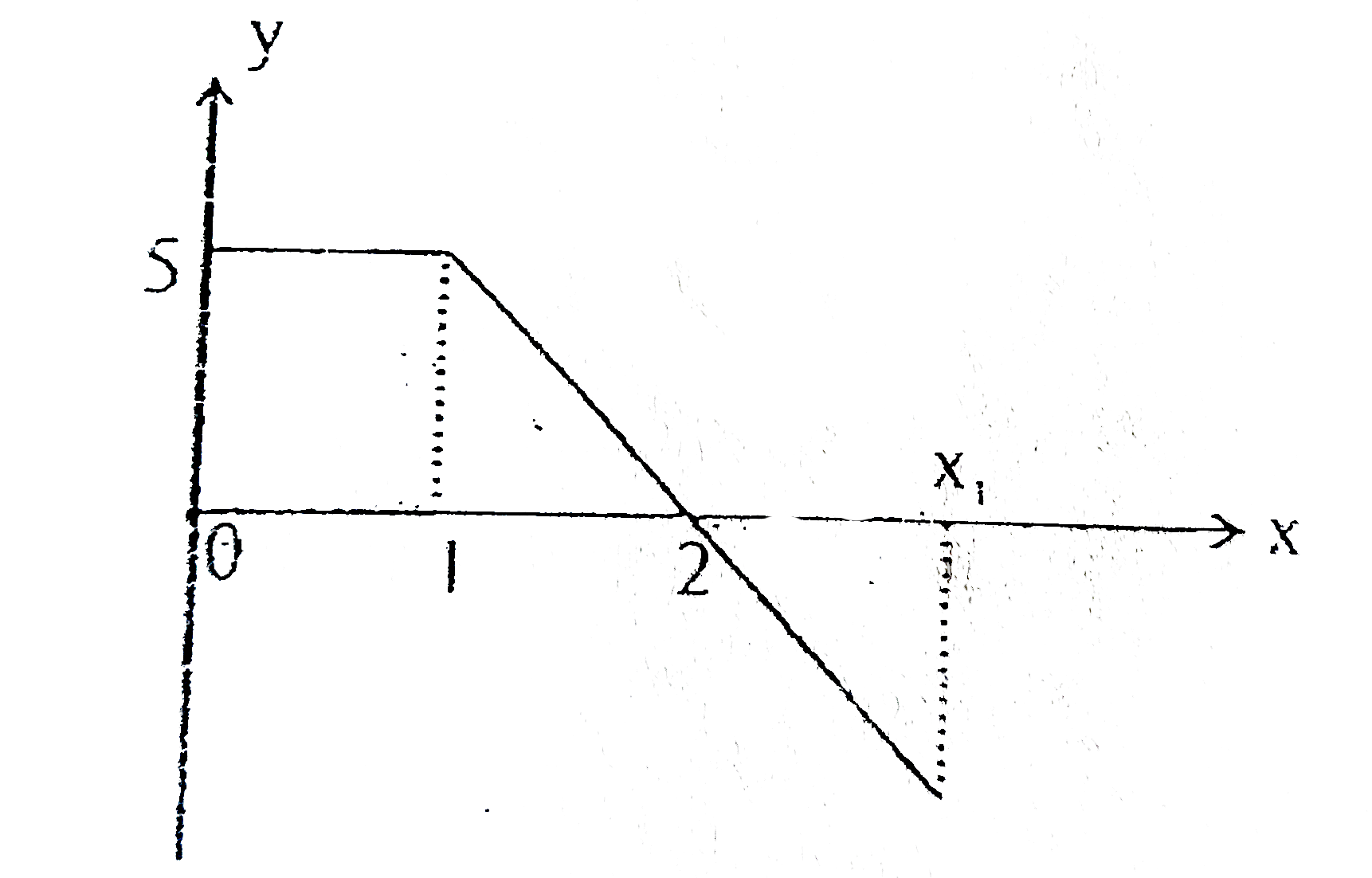
View SolutionWhich of the following equation is best representation of given graph's?
View SolutionConvert the angle from degree to radian :
30∘
View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.
View SolutionA disc is made to oscillate about a horizontal axis passing through one of its ends and its behaves like a second's pendulum. Determine its lengths.
View SolutionThe position of a particle moving along x-axis varies eith time t as x=4t−t2+1. Find the time interval(s) during which the particle is moving along positive x-direction.
View SolutionA particle moves along x-axis with acceleration a=6(t-1) where t is in second. If the particle is initially at the origin and it moves along positive x-axis with v_(0)=2m//s , find the nature of motion of the particle.
View SolutionPosition of a particle moving along x-axis is given by x=2+8t-4t^(2) . The distance travelled by the particle from t=0 to t=2 is:-
View SolutionIf the velocity of a particle moving along x-axis is given as v=(3t2−2t) and t=0, x=0 then calculate position of the particle at t=2sec.
View Solution[" Position of particle "],[" moving along x axis is "],[" given by "x=t^(3)+4t+2" .Here "x],[" is in metre and "t" is in "],[" seconds.Find "],[" displacement of particle "],[" from "t=2" to "t=4" sec."]
View SolutionA particle moves in a straight line and its position x and time t are related as follows: x=(2+t)1/2
Acceleration of the particle is given by
View SolutionThe position of a particle moving along a straight line is given by x =2 - 5t + t ^(3). Find the acceleration of the particle at t =2 s. (x is metere).
View SolutionThe position of a particle moving along a. straight line is given by x=2−5t+t3 The acceleration of the particle at t = 2 sec. is ...... Here x is in meter.
View Solutionएक कण, जो कि x-अक्ष के अनुदिश गति कर रहा है, का समीकरण है x=u(t−2)+a(t−2)2 एक कण, जो कि X-अक्ष के अनुदिश गति कर रहा है, का समीकरण है x=u(t−2)+a(t−2)2
View SolutionThe position of a particle along x-axis at time t is given by x=1 + t-t^2 . The distance travelled by the particle in first 2 seconds is
View SolutionA particle moves along x-axis obeying the equation x=t(t-1)(t-2), where x (in metres) is the position of the particle at any time t (in seconds). The displacement when the velocity of the particle is zero, is
View Solution

