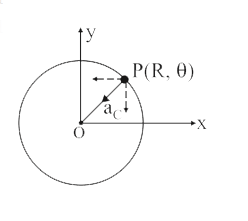
For a particle in uniform circular motion the acceleration a at a point P(R,θ) on the circle of radius R is (here 'v' is the speed of the particle and θ is measured from the x-axis)
v2Rˆi+v2Rˆj
−v2Rcosθˆi+v2Rsinθˆj
−v2Rsinθˆi+v2Rcosθˆj
−v2Rcosθˆi−v2Rsinθˆj
The correct Answer is:D
Step by step video solution for For a particle in uniform circular motion the acceleration a at a point P(R,θ) on the circle of radius R is (here 'v' is the speed of the particle and θ is measured from the x-axis) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (COLLISION AND CENTRE OF MASS )
12 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (ROTATIONAL MOTION)
72 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (WORK POWER & ENERGY)
34 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Video
Similar Questions
A disc of radius r is cut from a larger disc of radius 4r in such a way that the edge of the hole touches the edge of the disc. Locate the centre of mass of the residual disc.
View SolutionThe position (x) of a particle of mass 2 kg moving along x-axis at time t is given by x=(2t3) metre. Find the work done by force acting on it in time interval t=0 to t=2 is :-
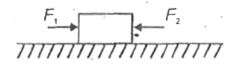
View SolutionA block of mass 2 kg is placed on a smooth horizontal surface. Two force F1=20N and F2=5N start acting on the block in opposite directions as shown. If block gets displaced by m in the direction of new force then work done by F2 is
View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.
View SolutionA disc is made to oscillate about a horizontal axis passing through one of its ends and its behaves like a second's pendulum. Determine its lengths.
View SolutionFor a particle in uniform circular motion , the acceleration →a at a point p(R,θ) on the circle of radiu R is ( Here θ is measured from the x−aξs )
View SolutionA particle is moving on a circular path of radius R with constant speed v. During motion of the particle form point A to point B
View Solutionएकसमान वृतीय गति में एक कण के लिये, R त्रिज्या के व्रत पर बिंदु P(R,θ) पर त्वरण →a ( यहां θ, X-अक्स से नापा गया है ) है :
View SolutionFor a particle in uniform circular motion the acceleration →a at a point P(R,θ) on the circle of radius R is : ( here θ is measured from the x- axis )
View SolutionA particle is moving around a circular path with uniform angular speed (x) . The radius of the circular path is (r). The acceleration of the particle is:
View SolutionFor a particle in uniform circular motion the acceleration a at a point P(R,θ) on the circle of radius R is (here 'v' is the speed of the particle and θ is measured from the x-axis)
View SolutionFor a particle in uniform circular motion, the acceleration →a at a point P(R,θ) on the circle of radius R (Here is measured from the x-axis) is
View SolutionA particle is moving on a circular path of radius R with constant speed v. During motion of the particle form point A to point B

View Solutionएकसमान वृत्तीय गति के कण के लिए, R त्रिज्या के वृत्त पर बिंदु P(R,θ) पर त्वरण →a है: (यहाँ θ, x- अक्ष से मापा जाता है)
View SolutionFor a particle in uniform circular motion , the acceleration →a at a point p(R,θ) on the circle of radiu R is ( Here θ is measured from the x−aξs )
View SolutionFor a particle in uniform circular motion the acceleration →a at a point P(R,θ) on the circle of radius R is : ( here θ is measured from the x- axis )

View Solution

