The variation in the speed of the planet in their orbits about the sun can be explained on the basic of the conservation of :-
Angular kinetic energy
Linear momentum
Angular momentum
None of these
The correct Answer is:C
To solve the question regarding the variation in the speed of planets in their orbits around the sun, we will follow these steps:
1. Understanding Planetary Motion:
- Planets move in elliptical orbits around the sun, with the sun located at one of the foci of the ellipse.
2. Identifying Key Points:
- In the elliptical orbit, there are two significant points:
- Perigee: The point where the planet is closest to the sun.
- Apogee: The point where the planet is farthest from the sun.
3. Speed Variation:
- At perigee, the speed of the planet (let's denote it as vp) is maximum.
- At apogee, the speed of the planet (let's denote it as va) is minimum.
4. Central Forces and Torque:
- The gravitational force between the sun and the planet acts as a central force directed towards the sun.
- Since the force is central, the net torque about the sun is zero. This is because the torque τ is given by τ=r×F, where r is the distance vector from the sun to the planet and F is the gravitational force. Since these vectors are anti-parallel at any point in the orbit, τ=0.
5. Conservation of Angular Momentum:
- The fact that the net torque is zero implies that angular momentum is conserved.
- Angular momentum L is given by L=mvr, where m is the mass of the planet, v is its speed, and r is the distance from the sun.
6. Relationship Between Speed and Distance:
- Since angular momentum is conserved, we can express this as mvprp=mvara, where rp and ra are the distances from the sun at perigee and apogee, respectively.
- This leads to the relationship vprp=vara, which implies v∝1r. Hence, as the distance r decreases (at perigee), the speed v increases, and vice versa.
7. Conclusion:
- The variation in the speed of the planets in their orbits can be explained by the conservation of angular momentum.
Final Answer:
The variation in the speed of the planets in their orbits about the sun can be explained on the basis of the conservation of angular momentum.
---
- Planets move in elliptical orbits around the sun, with the sun located at one of the foci of the ellipse.
- In the elliptical orbit, there are two significant points:
- Perigee: The point where the planet is closest to the sun.
- Apogee: The point where the planet is farthest from the sun.
- At perigee, the speed of the planet (let's denote it as vp) is maximum.
- At apogee, the speed of the planet (let's denote it as va) is minimum.
- The gravitational force between the sun and the planet acts as a central force directed towards the sun.
- Since the force is central, the net torque about the sun is zero. This is because the torque τ is given by τ=r×F, where r is the distance vector from the sun to the planet and F is the gravitational force. Since these vectors are anti-parallel at any point in the orbit, τ=0.
- The fact that the net torque is zero implies that angular momentum is conserved.
- Angular momentum L is given by L=mvr, where m is the mass of the planet, v is its speed, and r is the distance from the sun.
- Since angular momentum is conserved, we can express this as mvprp=mvara, where rp and ra are the distances from the sun at perigee and apogee, respectively.
- This leads to the relationship vprp=vara, which implies v∝1r. Hence, as the distance r decreases (at perigee), the speed v increases, and vice versa.
- The variation in the speed of the planets in their orbits can be explained by the conservation of angular momentum.
The variation in the speed of the planets in their orbits about the sun can be explained on the basis of the conservation of angular momentum.
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Properties of Matter & Fluid Mechanics)(Elasticity)
20 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Properties of Matter & Fluid Mechanics)(Fluid Dynamics + Viscosity)
18 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (ROTATIONAL MOTION)
72 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Video
Similar Questions
Consider a hypothetical solar system, which has two identical massive suns each of mass M and radius r, seperated by a seperation of 2√3R (centre to centre). (R>>r). These suns are always at rest. There is only one planet in this solar system having mass m. This planet is revolving in circular orbit of radius R such that centre of the orbit lies at the mid point of the line joining the centres of the sun and plane of the orbit is perpendicular to the line joining the centres of the sun. Whole situation is shown in the figure.
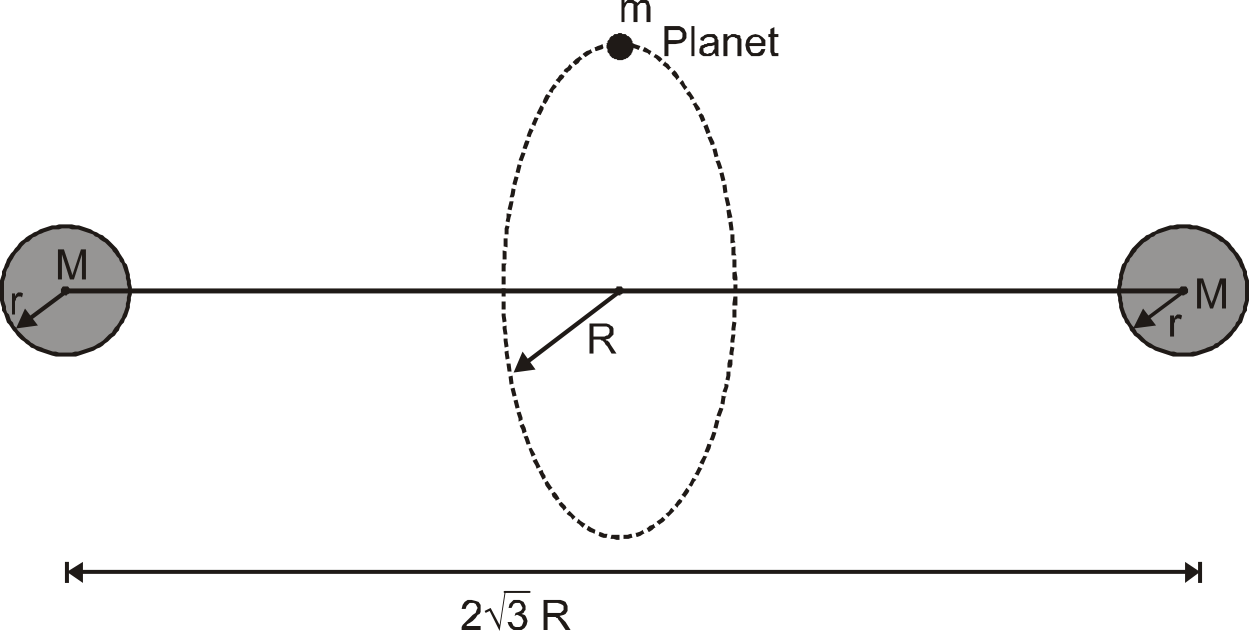
Q. Speed of the planet is
View SolutionConsider a hypothetical solar system, which has two identical massive suns each of mass M and radius r, seperated by a seperation of 2√3R (centre to centre). (R gtgtgtr). These suns are always at rest. There is only one planet in this solar system having mass m. This planet is revolving in circular orbit of radius R such that centre of the orbit lies at the mid point of the line joining the centres of the sun and plane of the orbit is perpendicular to the line joining the centres of the sun. Whole situation is shown in the figure.
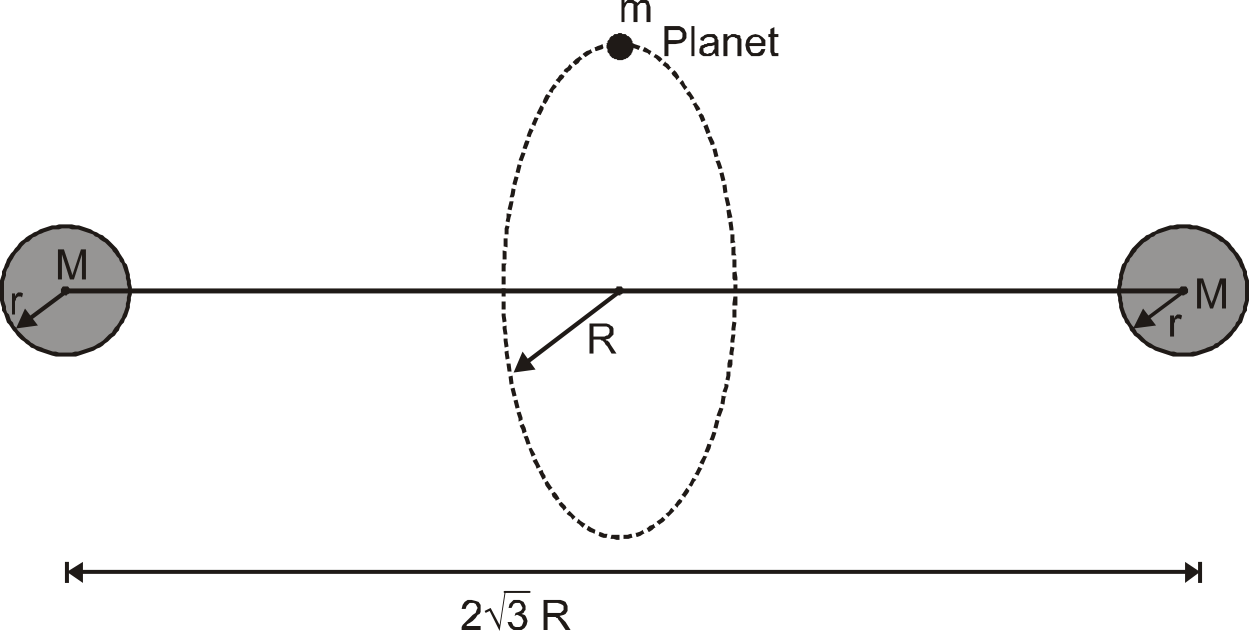
View Solution
Knowledge Check
Assertion : A central force is such that the force on the planet is along the vector joining the sun and the planet.
Reason : Conservation of angular momentum is valid for any central force.AIf both assertion and reason are true and reason is the correct explanation of assertionBIf both assertion and reason are truebut reason is not the correct explanation of assertionCIf assertion is true but reason is falseDIf both assertion and reason are false.A planet is revolving in an elliptical orbit around the sun. Its closest distance from the sun is r and the farthest distance is R. If the velocity of the planet nearest to the sun be v and that farthest away from the sun be V. then v/V is
AR2/r2Br2/R2CR/rDr/RA planet revolves around the sun in elliptical orbit of eccentricity 'e'. If 'T' is the time period of the planet then the time spent by the planet between the ends of the minor axis and major axis close to the sun is
ATπ2eBT(2eπ−1)CTe2πDT(14−e2π)
According to Kepler's second law, the radius vector to a planet from the Sun sweeps out equal areas in equal intervals of time. This law is a consequence of the conservation of ______________.
View SolutionA planet of mass 4 times earth spins about itself and completes one rotation is 96 hours . The radius of a secondary stationary satellite about this planet in comparisons to the radius of the geostationary orbit around the earth is
View SolutionA body is moving in a low circular orbit about a planet of mass M and radius R. The radius of the orbit can be taken to be R itself. Then the ratio of the speed of this body in the orbit to the escape velocity from the planet is :
View SolutionA planet of mass m1 revolves round the sun of mass m2. The distance between the sun the planet is r. Considering the motion of the sun find the total energy of the system assuming the orbits to be circular.
View SolutionAssertion : For circular orbits, the law of periods is T2∝r3, where M is the mass of sun and r is the radius of orbit.
Reason : The square of the period T of any planet about the sum is proportional to the cube of the semi-major axis a of the orbit.
View Solution

