
A solid cylinder of mass M is attached to the spring by means of a frintionless pivot. The cylinder is placed on floor. Find the time period of small oscillation of the system, if the floor is sufficiently rought to prevent any slipping of cylinder. Assume stiffness of spring to be K.
2π√7M5K
2π√5M3K
2π√3M2K
2π√MK
The correct Answer is:C
Let the cylinder is slightly displaced from mean position
the total energy of the system when elongation in spring is x.
E=12kx2+12Mv2+12×(12MR2)ω2
Differentiating the above expression we get
2kxdxdt+M2vdvdt+12MR22vR2dvdt=0
2kx+(2M+M)dvdt=0
dvdt=−(2K3M)x
T=2π√3M2k
Similar Questions
A solid cylinder is attached to a horizonatal massless spring as shwn in figure.If the cyclinder rolls without slipping, the time period of oscillation of the cyclinder is
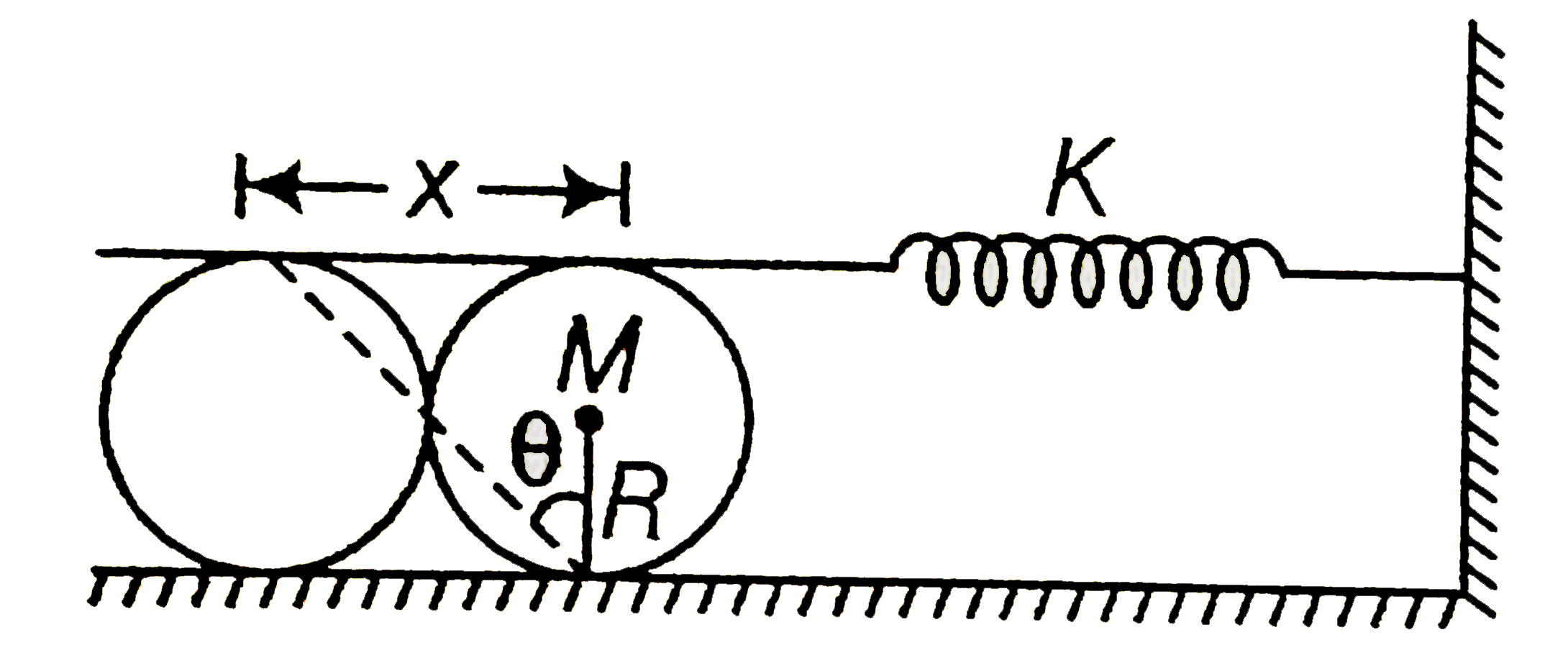
View SolutionA solid cylinder of mass m length L and radius R is suspended by means of two ropes of length l each as shown. Find the time period of small angular oscillations of the cylinder about its axis AA'
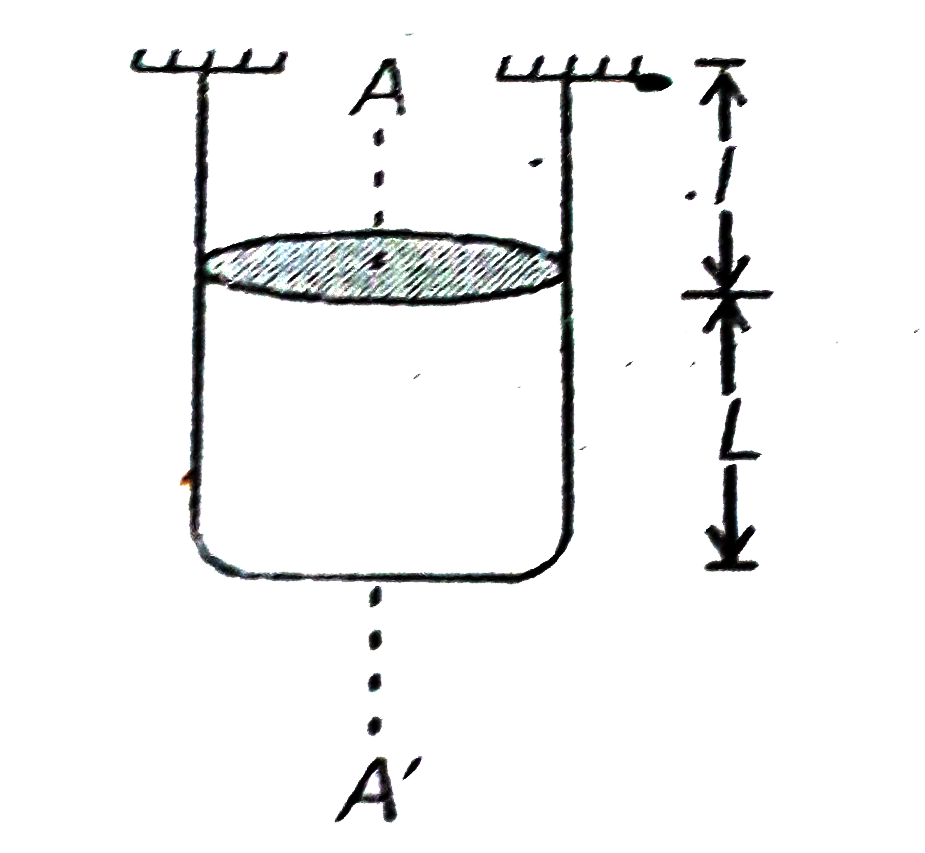
View SolutionSpring mass system is shown in figure. find the time period of vertical oscillations. The system is in vertical plane.

View SolutionA block of mass m hangs from three springs having same spring constant k. If the mass is slightly displaced downwards, the time period of oscillation will be

View SolutionA solid uniform cylinder of mass m performs small oscillations due to the action of two springs of stiffness k each (figure). Find the period of these oscillation in the absence of sliding.
x
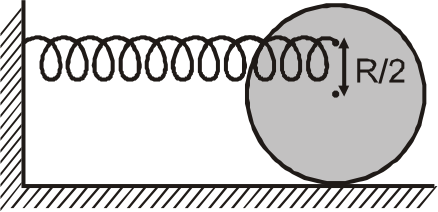
View SolutionA uniform disc of mass m is attached to a spring of spring constant k as shown in figure and there is sufficient friction to prevent slipping of disc. Time period of small oscillations of disc is:
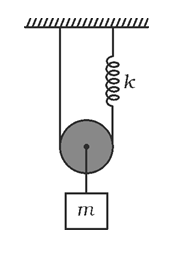
View SolutionFind the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
View SolutionThe ratio of the time periods of small oscillation of the insulated spring and mass system before and after charging the masses is
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA solid sphere of mass m is attached to a light spring of force constant k so that it can roll without slipping along a horizontal surface. Calculate the period of oscillation made by sphere.

View Solution
