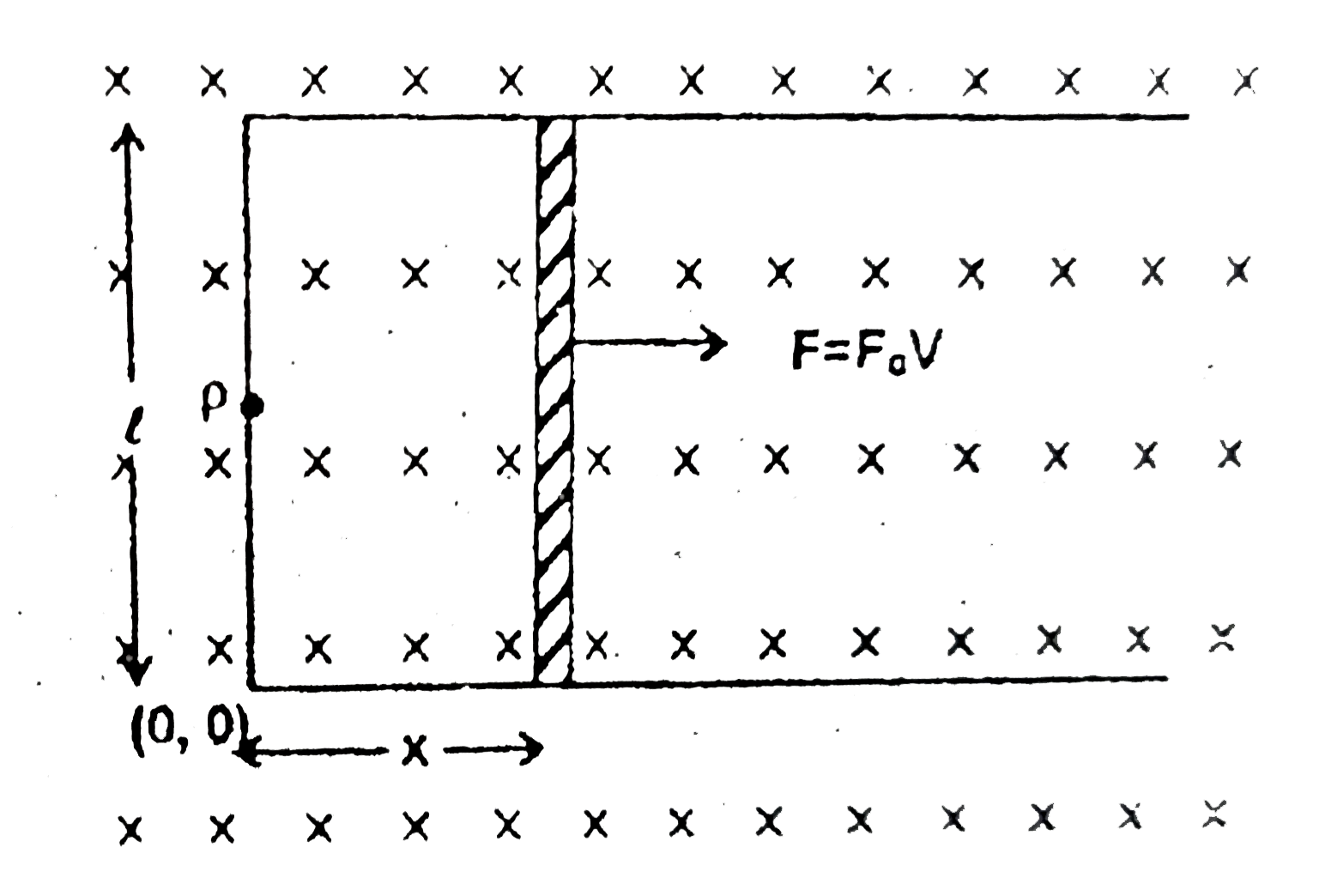
Two infinite parallel wire, having the cross sectional area 'a' and resistivity 'k' are connected at a junction point 'p' (as shown in the figure). A slide wire of negligible resistance and having mass 'm' and length 'l' can slide between the parallel wires, without any frictional resistance. If the system of wires is introduced to a magnetic field of intensity 'B' (into the plane of paper) and the slide wire is pulled with a force which varies with the velocity of the slide wire as F=F0v, then find the velocity of the slide wire as a function of the distance travelled.
(The slide wire is initially at origin and has a velocity v0)

At any given instance of time the slide wire is at distance x from origin, then the resistance of the circuit is R=k(2x+l)a
If the velocity of slide wire is v, then the emf generated is Blv so we have
BlV−ka(2x+l)I=0
Or, I=Blak(v2x+l)
This current exerts magnetic force in the wire given by F'
So, F'=IlB=Blak(v2x+l)lB=B2l2ak(v2x+l)
Since, F−F'=mdvdt
So F0v−B2l2ak(v2x+l)=mvdvdx
⇒F0m−B2l2akm(12x+l)=dvdx
⇒∫x0[F0m−B2l2akm(12x+l)]dx=∫VV0dv
F0mx−B2l2a2km{ln(2x+ll)}+v0=v
Similar Questions
A wire having mass m and length 1 can freely slide on a pair or parallel smooth horizontal rails placed in vertical magnetic field B. The rails are connected by a capacitor of capacitance C . The electric resistance of the rails and the wire is zero .If a constant force F acts on the Wire as shown in the figure . Then ,the acceleration of the wire can be given as

View SolutionA battery is connected across a resistance wire of uniform cross-section . If another resistance wire is connected in parallel, then the intensity of electric field in the first wire will
View SolutionA straight wire of length l can slide on two parallel plastic rails kept in a horizontal plane with a separation d. The coefficient of friction between the wire and the rails is μ. If the wire carries a current I, what minimum magnetic field should exist in the space in order to slide the wire on the rails.
View SolutionA wire of mass m and length I can freely slide on a pair of parallel, smooth, horizontal rails placed in a vertical magnetic field B . The rails are connected by a capacitor of capacitance C. The electric resistance of the rails and the wire is zero. If a constant force F acts on the wire as shown in the figure, find the acceleration of the wire.
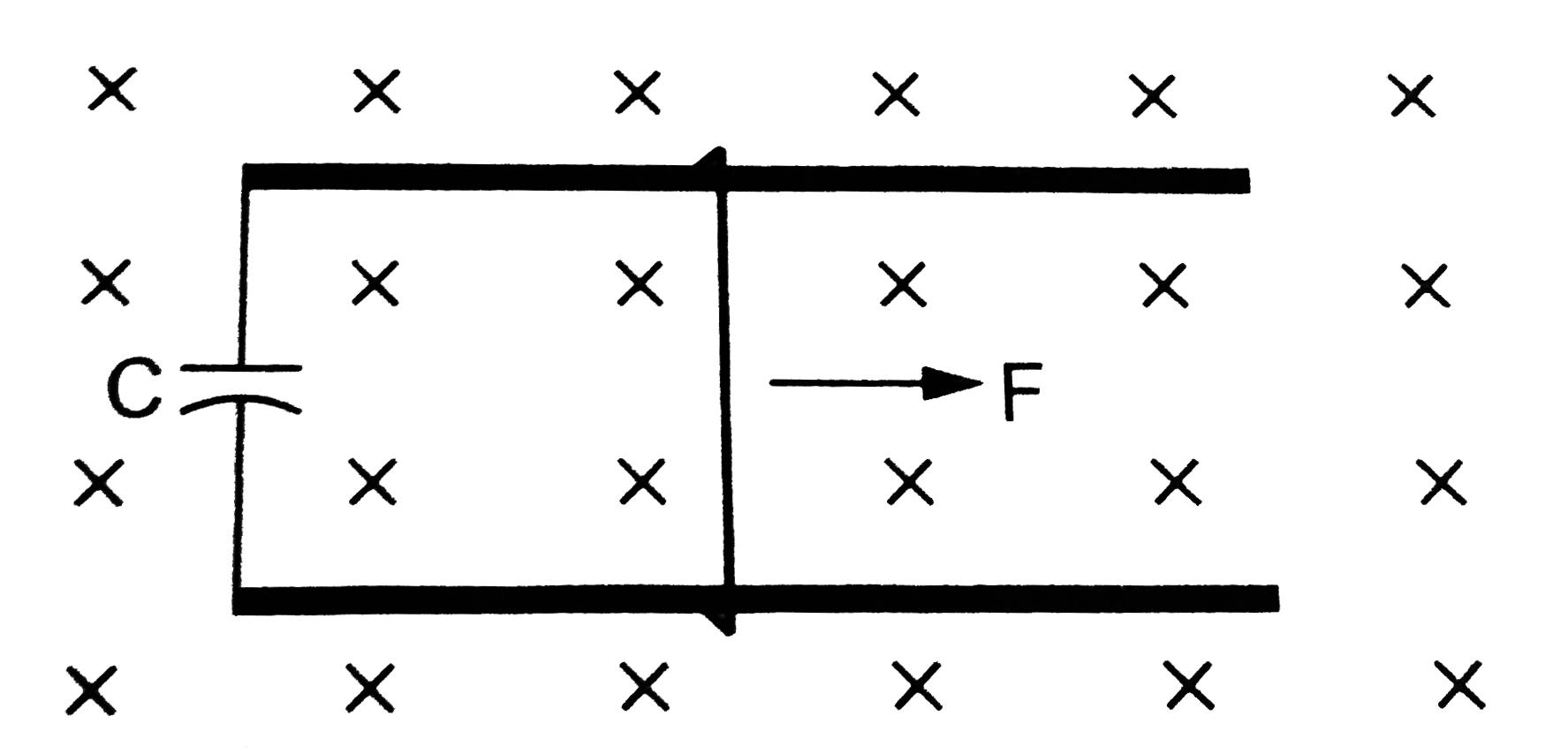
View SolutionA conducting wire of length l and mass m can slide without friction on two parallel rails and is connected to capacitance C. The whole system lies in a magnetic field B and a constant force F is applied to the rod. Then
View SolutionA conducting wire of length l and mass m can slide without friction on two parallel rails and is connected to capacitance C . The whole system lies in amagnetic field B and a constant force F is applied to the rod . Then
View SolutionA long straight wire carries a current I_(0) , at distance a and b=3a from it there are two other wires, parallel to the former one, which are interconnected by a resistance R (figure).A connector slides without friction along the wires with a constant velocity v .Assuming the resistance of the wires,the connector, the sliding contacts and the self-inductance of the frame to be negligible. The point of application (distance from the long wire) of magnetic force on sliding wire due to the long wire is (2a)/(lnx) from long wire.Then find out value of x .
View SolutionA wire of length l , mass m and resistance R slides without any friction down the parallel conducting rails of negligible resistance . The rails are connected to each other at the bottom by a resistanceless rail parallel to the wire so that the wire and the rails form a closed rectangualr conducting loop. The plane of the rails makes an angle theta with the horizontal and a uniform vertical magnetic field of the inducetion B exists throughout the rregion. Find the steady state velocity of the wire.
View Solution

