A particle of mass m moves on the x-axis under the influence of a force of attraction towards the origin O given by F=−kx2ˆi. If the particle starts from rest at x = a. The speed of it will attain to reach at distance x from the origin O will be
√2km[a−xax]1/2
√2km[a+xax]1/2
√km[axa−x]
√m2k[a−xax]1/2
The correct Answer is:A
To solve the problem, we need to find the speed v of a particle of mass m moving under the influence of a force F=−kx2^i, starting from rest at x=a and reaching a distance x from the origin O.
1. Identify the Force and Relation to Acceleration:
The force acting on the particle is given by:
F=−kx2
According to Newton's second law, we can relate force to acceleration:
F=m⋅a
where a=dvdt.
2. Express Acceleration in Terms of Velocity:
We can express acceleration a as:
a=vdvdx
Thus, we can rewrite the force equation as:
m⋅vdvdx=−kx2
3. Rearranging the Equation:
Rearranging gives:
vdv=−km1x2dx
4. Integrating Both Sides:
We will integrate both sides. The left side integrates from 0 to v (since the particle starts from rest) and the right side integrates from a to x:
∫v0vdv=−km∫xa1x2dx
5. Calculating the Integrals:
The left side becomes:
v22
The right side can be integrated as follows:
−km(−1x)xa=−km(−1x+1a)=km(1x−1a)
6. Setting the Integrals Equal:
Equating both sides gives:
v22=km(1x−1a)
7. Solving for v2:
Multiplying both sides by 2:
v2=2km(1x−1a)
8. Finding v:
Taking the square root to find v:
v=√2km(1x−1a)
Final Result:
The speed v of the particle when it reaches a distance x from the origin is:
v=√2km(1x−1a)
The force acting on the particle is given by:
F=−kx2
According to Newton's second law, we can relate force to acceleration:
F=m⋅a
where a=dvdt.
We can express acceleration a as:
a=vdvdx
Thus, we can rewrite the force equation as:
m⋅vdvdx=−kx2
Rearranging gives:
vdv=−km1x2dx
We will integrate both sides. The left side integrates from 0 to v (since the particle starts from rest) and the right side integrates from a to x:
∫v0vdv=−km∫xa1x2dx
The left side becomes:
v22
The right side can be integrated as follows:
−km(−1x)xa=−km(−1x+1a)=km(1x−1a)
Equating both sides gives:
v22=km(1x−1a)
Multiplying both sides by 2:
v2=2km(1x−1a)
Taking the square root to find v:
v=√2km(1x−1a)
The speed v of the particle when it reaches a distance x from the origin is:
v=√2km(1x−1a)
Similar Questions
A particle of mass m moves on positive x-axis under the influence of force acting towards the origin given by −kx2ˆi. If the particle starts from rest at x=a, the speed it will attain when it crosses the origin is
View SolutionA particle moves along x-axis from x=0 to x=2 m under the influence of a force F (in N) given by F=3x2+2x−5. Calculate the work done
View SolutionA particle moves along the X-axis x=0 to x=5 m under the influence of a force given by F=10−2x+3x2. Work done in the process is
View SolutionA particle moves along the x-axis from x=0 to x=5m under the influence of a given by F=7−2x+3x2. The work done by the applied force to the particle is.
View SolutionA particle moves along the X-axis from x=0 to x=5 m under the influence of a force given by F=7−2x+3x2. Find the work done in the process.
View SolutionA particle of mass m moves from rest under the action of a constant force F which acts for two seconds. The maximum power attained is
View SolutionA particle is moving along the axis under the influnence of a force given by F=−5x+15. At time t=0, the particle is located at x=6 and having zero velocity it take 0.5 second to reach the origin for the first time. The equation of motion of the particle can be respected by
View Solution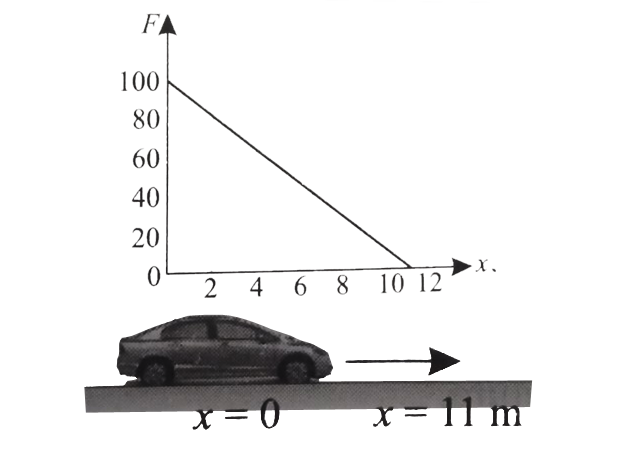
A toy car of mass 5 kg moves up a ramp under the influence of force F plotted against displacement x. The maximum height attained is given by
View SolutionA particle moves along X-axis from x=0 to x=1 m under the influence of a force given by F=3x2+2x−10. Work done in the process is
View SolutionA particle moves along X-axis from x=0 to x=1 m under the influence of a force given by F=3x2+2x−10. Work done in the process is
View Solution

