In a R, L, C circult, three elements is connected in series by an ac source. If frequency is less than resonating frequency then net impedance of the circuit will be
capacitive
inductive
capacitive or inductive
pure resistive
The correct Answer is:A
To solve the problem of finding the net impedance of an RLC circuit connected in series with an AC source when the frequency is less than the resonant frequency, we can follow these steps:
Step 1: Understand the Components
In an RLC circuit, we have:
- R: Resistance
- L: Inductance
- C: Capacitance
The circuit is connected in series to an AC source.
Step 2: Define Impedance
The net impedance (Z) of a series RLC circuit is given by the formula:
Z=√R2+(XL−XC)2
where:
- XL is the inductive reactance, given by XL=ωL
- XC is the capacitive reactance, given by XC=1ωC
Step 3: Understand Resonant Frequency
The resonant frequency (ωr) is defined as:
ωr=1√LC
Step 4: Analyze the Given Condition
The problem states that the frequency (ω) is less than the resonant frequency (ωr):
ω<ωr
Step 5: Determine Reactances
Since ω<ωr:
- The inductive reactance XL=ωL will be smaller because ω is less.
- The capacitive reactance XC=1ωC will be larger because ω is less.
Thus, we conclude:
XC>XL
Step 6: Calculate the Net Impedance
Since XC>XL, we can express the difference as:
XC−XL>0
Substituting this back into the impedance formula:
Z=√R2+(XL−XC)2=√R2+(−(XC−XL))2=√R2+(XC−XL)2
This indicates that the circuit behaves more like a capacitive circuit.
Step 7: Conclusion
When the frequency is less than the resonant frequency, the net impedance of the circuit will be dominated by the capacitive reactance, indicating that the circuit is capacitive in nature.
Final Answer
The net impedance of the circuit will be:
- Capacitive (indicating that Z is influenced more by XC than XL).
---
In an RLC circuit, we have:
- R: Resistance
- L: Inductance
- C: Capacitance
The net impedance (Z) of a series RLC circuit is given by the formula:
Z=√R2+(XL−XC)2
where:
- XL is the inductive reactance, given by XL=ωL
- XC is the capacitive reactance, given by XC=1ωC
The resonant frequency (ωr) is defined as:
ωr=1√LC
The problem states that the frequency (ω) is less than the resonant frequency (ωr):
ω<ωr
Since ω<ωr:
- The inductive reactance XL=ωL will be smaller because ω is less.
- The capacitive reactance XC=1ωC will be larger because ω is less.
XC>XL
Since XC>XL, we can express the difference as:
XC−XL>0
Z=√R2+(XL−XC)2=√R2+(−(XC−XL))2=√R2+(XC−XL)2
When the frequency is less than the resonant frequency, the net impedance of the circuit will be dominated by the capacitive reactance, indicating that the circuit is capacitive in nature.
The net impedance of the circuit will be:
- Capacitive (indicating that Z is influenced more by XC than XL).
Similar Questions
If resistance R =10Ω, inductance L = 2 mH and capacitance C=5μF are connected in series to an AC source of frequency 50 Hz, then at resonance the impedance of circuit is
View SolutionIn a series LCR circuit resonance of frequency is the half of the frequency of source.The nature of the circuit is
View Solution
Knowledge Check
At resonance frequency the impedance in series LCR circuit is
AmaximumBminimumCzeroDinfinityAt resonant frequency the current amplitude in series LCR circuit is
AmaximumBminimumCzeroDinfinityTo reduce the resonant frequency in an LCR series circuit with a generator
Athe generator frequency should be reduced.Banother capacitor should be added in parallel to the first.Cthe iron core of the inductor should be removed.Ddielectric in the capacitor should be removed.
The current through an inductor of impedance 10Ω lags behind the voltage by a phase of 60∘ when just the inductor is connected to the ac source. Now the inductor is connected to a 5Ω resistance in series, then the net impedance of the circuit is
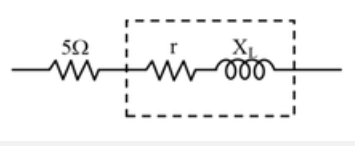
View SolutionIn a circuit containing R and L , as the frequency of the impressed AC increase, the impedance of the circuit
View SolutionIn a series L-C-R circuit shown in the figure , what is the resonance frequency and the current at the resonating frequency?
View SolutionTo reduce the resonant frequency in an LCR series circuit with a generator
View SolutionTo reduce the resonant frequency in an LCR series circuit with a generator
View Solution
