A uniform square plate ABCD has mass M side length a. It is sliding on a horizontal smooth surface with a velocity of→v=v0(4ˆi+2ˆj). There is no rotation. Vertex A of the plate is suddenly fixed by a nail. Calculate the velocity of centre of the plate immediately after this
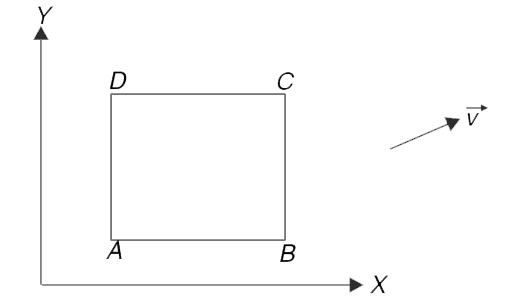
v0(2ˆi+4ˆj)
3v04(−ˆi)+3v04ˆj
3v02ˆi−3v02ˆj
3v0ˆi−3v0ˆj
The correct Answer is:B
Step by step video solution for A uniform square plate ABCD has mass M side length a. It is sliding on a horizontal smooth surface with a velocity ofvec(v) = v_(0) (4 hat(i) + 2 hat(j)). There is no rotation. Vertex A of the plate is suddenly fixed by a nail. Calculate the velocity of centre of the plate immediately after this by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023समान प्रश्न
A uniform cube of mass m and edge a moves on a horizontal surface along the positive x-axis, with initial velocity v0. Then
View SolutionA ring of mass m sliding on a smooth surface with velocity v0 enters rough surface with coefficient of kinetic friction μk, then
View SolutionA smooth sphere is moving on a horizontal surface with velocity vector 3ˆi+ˆj immediately before it hits a vertical wall. The wall is parallel to the vector ˆj and the coefficient of restitution between the wall and sphere is 13. The velocity vector of the sphere after it hits the wall is :-
View SolutionA uniform ring of radius R is given a back spin of angular velocity V0/2R and thrown on a horizontal rough surface with velocity of centre to be V0. The velocity of the centre of the ring when it starts pure rolling will be
View SolutionA portion is fired from origin with velocity →v=v0ˆj+v0ˆk in a uniform magnetic field →B=B0ˆj. In the subsequent motion of the proton
View SolutionA conductor AB of length l moves in xy plane with velocity →v=v0(ˆi−ˆj). A magnetic field →B=B0(ˆi+ˆj) exists in the region. The induced emf is
View SolutionA smooth sphere of mass m is moving on a horizontal plane with a velocity (3ˆi+ˆj) . It collides with smooth a vertical wall which is parallel to the vector ˆj . If coefficient of restitution e=12 then impulse that acts on the sphere is
View SolutionConsider an object of mass m moving in free space with velocity given by →v=v0cosωtˆi+v0sinωtˆj . Here v0 and ω are constants and t represents time. calculate force acting on object and angle between force and momentum.
View SolutionA particle leaves the origin with initial velocity →v0=11ˆi+14ˆjm/s. It undergoes a constant acceleration given by →a=−225ˆi+215ˆjm/s2.
When does the particle cross the y-axis ?
View SolutionA particle has an initial velocity of 3ˆi+4ˆj and an acceleration of 0.4ˆi+0.3ˆj. Its speed after 10s is :
View Solution

