The ratio of masses of a cubical block of wood and a chunk of concrete is 3/5 so that the combination just floats with entire volume submerged under water. If the specific gravity of wood is 0.5 then specific gravity of concrete will be
2.5
25
15
3
The correct Answer is:A
To solve the problem, we will follow these steps:
Step 1: Define the variables
Let:
- Mass of wood = 3x
- Mass of concrete = 5x
- Density of wood = ρ1
- Density of concrete = ρ2
- Density of water = ρw
Step 2: Write the buoyancy condition
Since the combination of wood and concrete just floats with the entire volume submerged, we can use the principle of buoyancy:
ρw⋅Vblock=Weight of the block
This means:
ρw⋅Vblock=mass of wood+mass of concrete
Step 3: Express the volume of the block
The volume of the block can be expressed as:
Vblock=Vwood+Vconcrete=3xρ1+5xρ2
The total mass of the block is:
mass of block=3x+5x=8x
Step 4: Set up the equation
From the buoyancy condition, we have:
ρw(3xρ1+5xρ2)=8x
We can cancel x from both sides (assuming x≠0):
ρw(3ρ1+5ρ2)=8
Step 5: Substitute the specific gravity of wood
The specific gravity of wood is given as 0.5, which means:
ρ1ρw=0.5⟹ρ1=0.5ρw
Step 6: Substitute ρ1 into the equation
Substituting ρ1 into the equation gives:
ρw(30.5ρw+5ρ2)=8
This simplifies to:
ρw(6+5ρ2)=8
Step 7: Divide by ρw
Dividing both sides by ρw gives:
6+5ρ2=8ρw
Step 8: Rearrange to find ρ2
Rearranging gives:
5ρ2=8ρw−6
5ρ2=8−6ρwρw
Thus,
ρ2=5ρw8−6ρw
Step 9: Find the specific gravity of concrete
The specific gravity of concrete is given by:
Specific Gravity of Concrete=ρ2ρw=58−6ρw
Substituting ρw=1 (as the specific gravity of water is 1):
Specific Gravity of Concrete=58−6=52=2.5
Final Answer
The specific gravity of concrete is 2.5.
---
Let:
- Mass of wood = 3x
- Mass of concrete = 5x
- Density of wood = ρ1
- Density of concrete = ρ2
- Density of water = ρw
Since the combination of wood and concrete just floats with the entire volume submerged, we can use the principle of buoyancy:
ρw⋅Vblock=Weight of the block
This means:
ρw⋅Vblock=mass of wood+mass of concrete
The volume of the block can be expressed as:
Vblock=Vwood+Vconcrete=3xρ1+5xρ2
The total mass of the block is:
mass of block=3x+5x=8x
From the buoyancy condition, we have:
ρw(3xρ1+5xρ2)=8x
We can cancel x from both sides (assuming x≠0):
ρw(3ρ1+5ρ2)=8
The specific gravity of wood is given as 0.5, which means:
ρ1ρw=0.5⟹ρ1=0.5ρw
Substituting ρ1 into the equation gives:
ρw(30.5ρw+5ρ2)=8
This simplifies to:
ρw(6+5ρ2)=8
Dividing both sides by ρw gives:
6+5ρ2=8ρw
Rearranging gives:
5ρ2=8ρw−6
5ρ2=8−6ρwρw
Thus,
ρ2=5ρw8−6ρw
The specific gravity of concrete is given by:
Specific Gravity of Concrete=ρ2ρw=58−6ρw
Substituting ρw=1 (as the specific gravity of water is 1):
Specific Gravity of Concrete=58−6=52=2.5
The specific gravity of concrete is 2.5.
Similar Questions
wood with specific gravity of less than 0.2 is
View Solutionwood with specific gravity of less than 0.05 occurs in
View SolutionThe specific gravity of SO3 vapour at0oC and 76 cmHg in grams/ litre is
View SolutionA piece of cork whose weight is 19 gm is attached to a bar of silver weighing 63 gm. The two together just not in water. The specific gravity of silver is 10-5. Find the specific gravity of the cork. Density of water = 1gmcm−3
View SolutionA concrete sphere of radius R has cavity of radius r which is packed with sawdust. The specific gravities of concrete and sawdust are respectively 2.4and0.3 for this sphere to float with its entire volume submerged under water. Ratio of mass of concrete to mass of swadust will be
View SolutionA cubical block of wood weighing 200 g has a lead piece fastened underneath. Find the mass of the lead piece which will just allow the block of float in water. Specific gravity of wood is 0.8 and that of lead is 11.3.
View SolutionA cubical block of ice floating in water has to suport metal piece weighing 0.5 kg. What can be the minimum edge of the block so that it does not sink in water/ specific gravity of ice=0.9.
View SolutionA cube of ice floats partly in water and partly in K.oil figure. Find the ratio of the volume of ice immersed in water to that in K.oil. Specific gravity of K.oil is 0.8 and that of ice is 0.9.
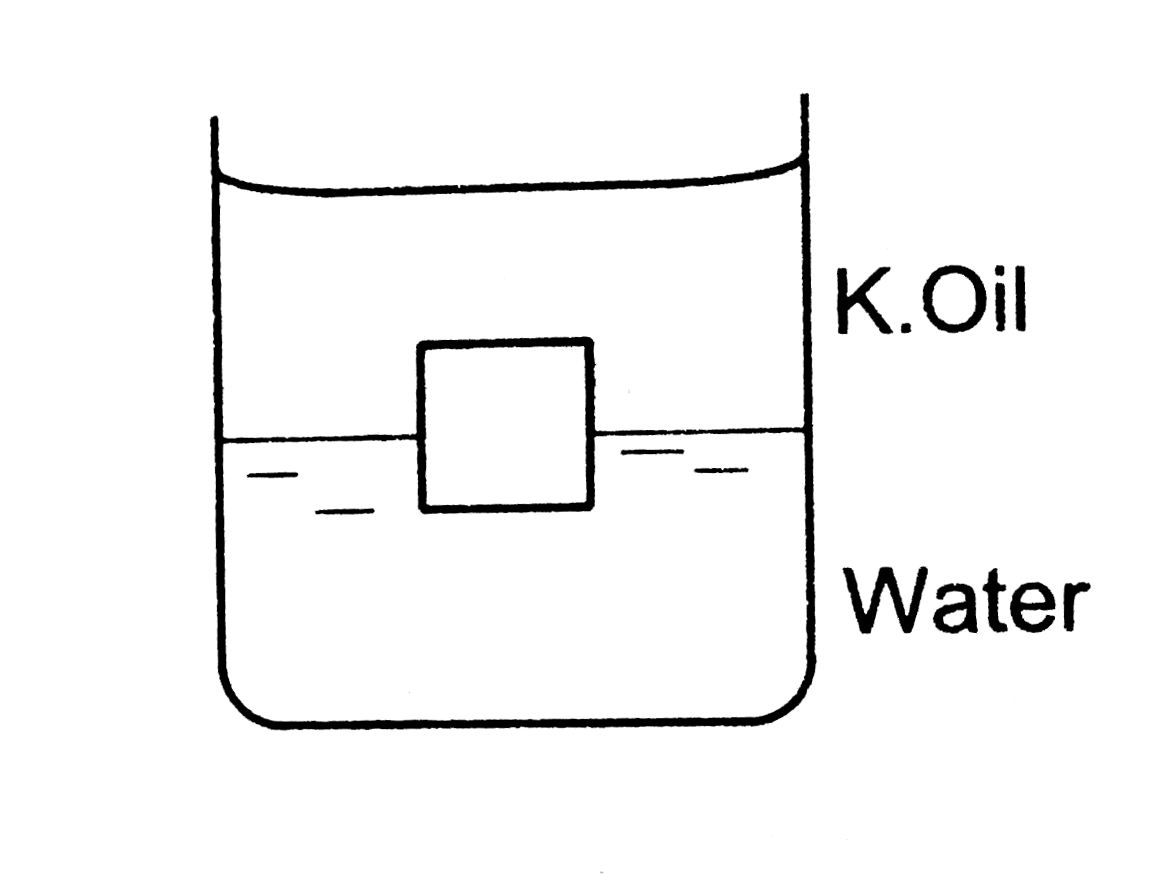
View SolutionA cubical block of ice floating in water has to support a metal piece weighing 0.5 kg. What can be the minimum edge of the block so that it does not sink in water? specific gravity of ice=0.9.
View SolutionA block of wood floats on water with 25 th of its volume above the water surface. Calculate the density of wood.
View Solution

