Consider the situation shown in the figure. A mass is hanging from a inextensible string which is passing over a pulley. The pulley itself is attached to a massless spring of stiffness k as shown in the figure. Find the time period of vertical oscillations of mass m if pulley is slightly displaced from its mean position. Assume that string does not slip over pulley.
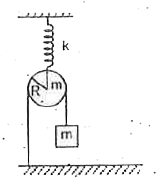
At equilibrium position let x0 be the deformation in the spring
∴x0=3mgk
Let the pulley is displaced by x then total energy of system
E=(−mgx+12mv2+12lω2)+(12m(2v)2−mg(h+2x))+12k(x0+x)2
As string does not slip over pulley so ω=v/r.
So E=(−mgx+12mv2+14mv2)+(2mv2−mg(h+2x)+12k(x0+x)2)
dEdt=0,∴0=−mg+mdvdt+m2dvdt−2mg+4mdvdt+k(x0+x)
⇒kx+(m+m2+4m)dvdt=0
⇒dvdt=2k11mx
⇒ω=√2k11morT=2π√11m2k
Similar Questions
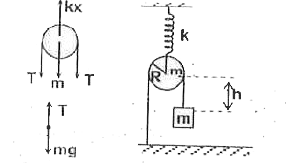
In the situation as shown in figure time period of small vertical oscillation of block will be - (String, springs and pulley are ideal)
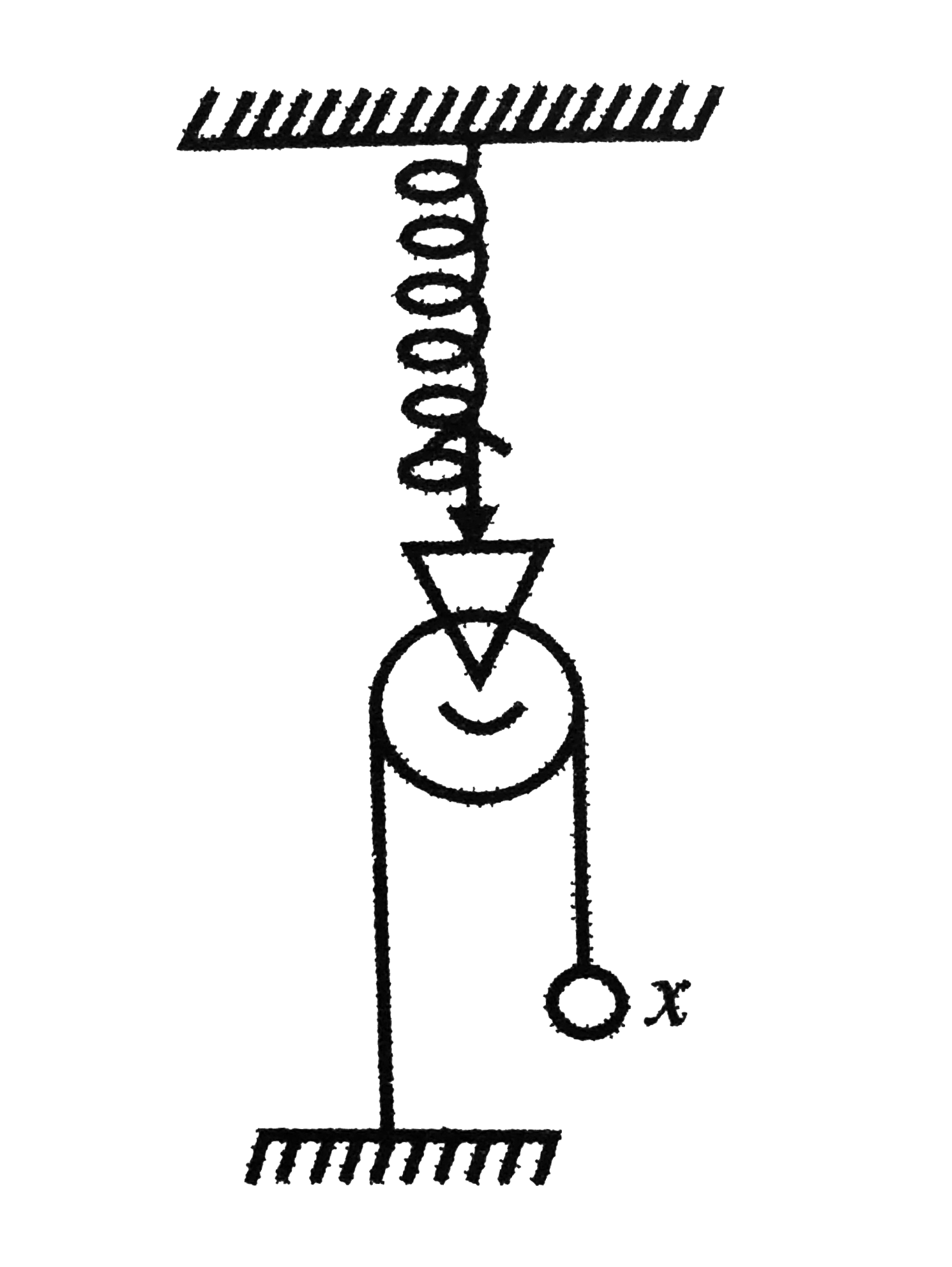
View SolutionFind the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.

View SolutionThe pulley shown in figure has a moment of inertias I about its axis and mass m. find the time period of vertical oscillation of its centre of mass. The spring has spring constant k and the string does not slip over the pulley.

View SolutionThe pulley shown in figure has a moment of inertias I about its xis and mss m. find the tikme period of vertical oscillastion of its centre of mass. The spring has spring constant k and the string does not slip over the pulley.

View SolutionThe string, spring and the pulley shown in figure are light. Find the time period of the mass m.

View SolutionThe time period of block of mass m is (Assume pulleys and string are massless)
_PHY_E06_345_Q01.png) .
.
View SolutionA body of mass m hangs by an inextensible string that passes over a smooth mass less pulley that is fitted with a light spring of stiffness k as shown in figure. If the body is released from rest and the spring is released, calculate the maximum elongation of the spring.
View SolutionConsider the situation shown in the figure. The surface is smooth and the string and the pulley are light. Find the acceleration of each block and tension in the string.

View SolutionThree blocks of masses m1,m2andm3 are connected as shown in the figure. All the surfaces are frictionless and the string and the pulleys are light. Find the acceleration of m1
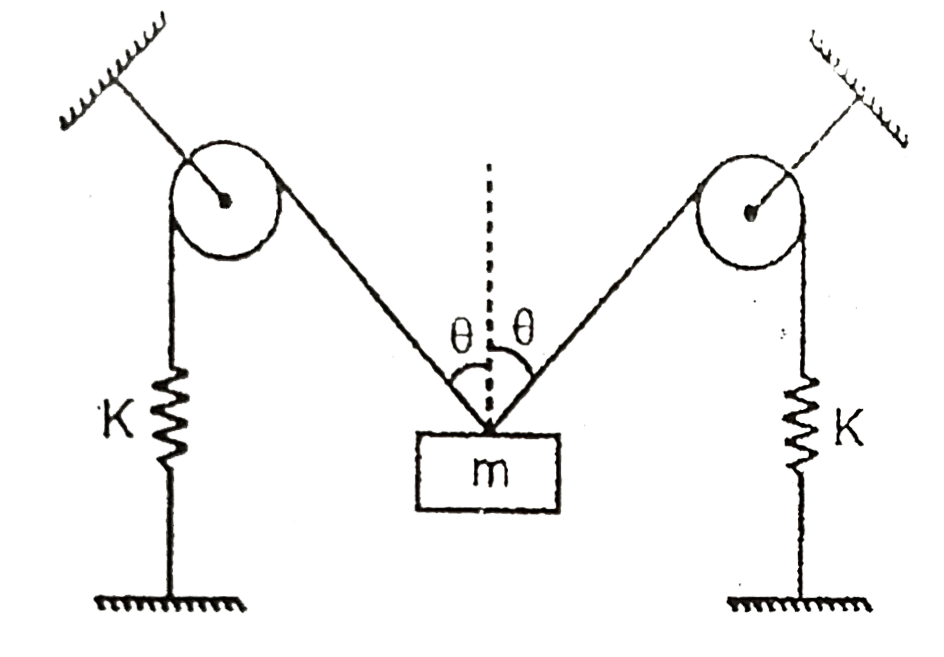
View SolutionA body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is

View Solution
