A cell of voltage V0 is connected across a capacitor of capacitance C. Now the space between the plates is filled with a material of dielectric constant K. Find ratio of charge appear on the plates of capacitor before and after filling.
To find the ratio of charge appearing on the plates of a capacitor before and after filling the space between the plates with a dielectric material, we can follow these steps:
1. Understanding the Initial Setup:
- We have a capacitor with capacitance C connected to a voltage source of voltage V0.
- The charge on the capacitor before filling the dielectric can be denoted as Q1.
2. Calculating Charge Before Filling:
- The charge Q1 on the capacitor can be calculated using the formula:
Q1=C⋅V0
3. Introducing the Dielectric:
- When the space between the plates of the capacitor is filled with a dielectric material with dielectric constant K, the capacitance of the capacitor increases.
- The new capacitance C′ after filling the dielectric is given by:
C′=K⋅C
4. Calculating Charge After Filling:
- The charge Q2 on the capacitor after filling with the dielectric can be calculated using the new capacitance:
Q2=C′⋅V0=(K⋅C)⋅V0=K⋅C⋅V0
5. Finding the Ratio of Charges:
- Now, we can find the ratio of the charge before filling to the charge after filling:
Q1Q2=C⋅V0K⋅C⋅V0
- Simplifying this expression, we find:
Q1Q2=1K
6. Final Result:
- Therefore, the ratio of the charge on the plates of the capacitor before and after filling is:
Ratio=1:K
- We have a capacitor with capacitance C connected to a voltage source of voltage V0.
- The charge on the capacitor before filling the dielectric can be denoted as Q1.
- The charge Q1 on the capacitor can be calculated using the formula:
Q1=C⋅V0
- When the space between the plates of the capacitor is filled with a dielectric material with dielectric constant K, the capacitance of the capacitor increases.
- The new capacitance C′ after filling the dielectric is given by:
C′=K⋅C
- The charge Q2 on the capacitor after filling with the dielectric can be calculated using the new capacitance:
Q2=C′⋅V0=(K⋅C)⋅V0=K⋅C⋅V0
- Now, we can find the ratio of the charge before filling to the charge after filling:
Q1Q2=C⋅V0K⋅C⋅V0
- Simplifying this expression, we find:
Q1Q2=1K
- Therefore, the ratio of the charge on the plates of the capacitor before and after filling is:
Ratio=1:K
Topper's Solved these Questions
- JEE MAIN 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2021Exercise:SECTION-A
Explore 80 Videos
- JEE MAIN 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2021Exercise:SECTION-B
Explore 40 Videos
- JEE MAINBook:JEE MAINS PREVIOUS YEARChapter:JEE MAINExercise:All Questions
Explore 473 Videos
- JEE MAIN 2022Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2022Exercise:Question
Explore 492 Videos
Similar Questions
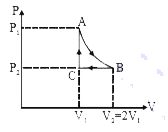
n mole a perfect gas undergoes a cyclic process ABCA (see figure) consisting of the following processes.
A→B: Isothermal expansion at temperature T so that the volume is doubled from V1 to V2=2V1 and pressure changes from P1 to P2
B→C : Isobaric compression at pressure P2 to initial volume V1
C→A : Isochoric change leading to change of pressure from P2 toP1 .
Total work done in the complete cycle ABCA is :
View SolutionThe coefficient of static friction between a wooden block of mass 0.5 kg and a vertical rough wall is 0.2. The magnitude of horizontal force that should be applied on the block to keep it adhere to the wall will be ____N.
View SolutionIf weight of an object at pole is 196 N then weight at equator is [g=10ms2 , radius of earth = 6400 Km]
View SolutionThe normal reaction 'N' for a vehicle of 800 kg mass, negotiating a turn on a 30∘ banked road at maximum possible speed without skidding is _______ ×103 kg m/s2.
View SolutionTwo parallel plate capacitors, each of capacitance 40 muF, are connected is series. The space between the plates of one capacitor is filled with a dielectric material of dielectric constant K =4. Find the equivalent capacitacne of the system.
View SolutionIn figure half of the space between the plates of a parallel plate capacitor is filled with dielectric material of constant K. Then which of the plots are possible?

View SolutionThe capacitance of a parallel plate capacitor is C when the region between the plate has air. This region is now filled with a dielectric slab of dielectric constant k. The capacitor is connected to a cell of emfE, and the slab is taken out
View SolutionThe plates of a parallel plate capacitor with no dielectirc are connected to a volatage source. Now a dielectric of dielectric constant K is inserted to fill the whose space between the plates with voltage source remainign connected to the capacitor-
View SolutionC तथा 2C धारिता के दो समान्तर प्लेट संधारित्र समांतर क्रम में V वोल्ट बैटरी से जोड़े जाते हैं। अब बैटरी हटा ली जाती हैं तथा संधारित्र C की प्लेटों के बीच k परावैघुतांक का पदार्थ भर दिया जाता हैं। संधारित्रों की प्लेटों के बीच विभवांतर ज्ञात कीजिये।
View SolutionA parallel plate capacitor A is filled with a dielectric whose dielectric constant varies with applied voltage as K = V. An identical capacitor B of capacitance C0 with air as dielectric is connected to voltage source V0=30V and then connected to the first capacitor after disconnecting the voltage source. The charge and voltage on capacitor.
View Solutionसमान्तर प्लेट संधारित्र की दोनों प्लेटों के बीच की जगह को एक परावैद्युत पदार्थ की प्लेट से पूरी तरह भर दिया जाता है। संधारित्र को आवेशित कर बैटरी से हटा लिया जाता है। इस परावैद्युत प्लेट को अब धीरे-धीरे संधारित्र के बाहर प्लेटों के समान्तर खींचा जाता है। इस तरह बाहर खींचे गये परावैद्युत प्लेट की लम्बाई x तथा संधारित्र की प्लेटों के विभवान्तर V के बीच खाचा गया ग्राफ होगा :
View SolutionTwo identical parallel plate capacitors A and B are connected to a battery of V volts with the switch S closed . The switch is now opened and the free space between the plates of the capacitors is filled with dielectric of dielectric constant K . Find the ratio of the total electrostatic energy stored in both capacitors before and after the introduction of the dielectric .
View SolutionTwo parallel plate capacitors, each of capacitance 40 muF, are connected is series. The space between the plates of one capacitor is filled with a dielectric material of dielectric constant K =4. Find the equivalent capacitacne of the system.
View SolutionA parallel plate capacitor A is filled with a dielectric whose dielectric constant varies with applied voltage as K = V. An identical capacitor B of capacitance C0 with air as dielectric is connected to voltage source V0=30V and then connected to the first capacitor after disconnecting the voltage source. The charge and voltage on capacitor.
View SolutionThe plates of a parallel plate capacitor with no dielectric are connected to a voltage source. Now a dielectric of dielectric constant K is inserted to fill the whole space between the plates with voltage source remaining connected to the capacitor.
View SolutionThe capacitance of a parallel plate capacitor is C when the region between the plate has air. This region is now filled with a dielectric slab of dielectric constant k. The capacitor is connected to a cell of emf E, and the slab is taken out
View Solution
