In right-angled ΔABC,DandE trisect BC. Find the value of 8 (AEAC)2−5(ADAC)2
1
2
3
4
The correct Answer is:C
To solve the problem, we need to find the value of 8(AEAC)2−5(ADAC)2 in the right-angled triangle ΔABC where points D and E trisect BC.
1. Identify the Triangle and Trisection Points:
- Let BC be trisected by points D and E. This means BD=DE=EC.
- Let BD=DE=EC=x. Therefore, BC=3x.
2. Apply the Pythagorean Theorem:
- In triangle ABD:
AD2=AB2+BD2=AB2+x2(Equation 1)
- In triangle ABE:
AE2=AB2+BE2=AB2+(BD+DE)2=AB2+(2x)2=AB2+4x2(Equation 2)
- In triangle ABC:
AC2=AB2+BC2=AB2+(3x)2=AB2+9x2(Equation 3)
3. Express AEAC and ADAC:
- From Equations 2 and 3, we have:
AE2AC2=AB2+4x2AB2+9x2
- From Equations 1 and 3, we have:
AD2AC2=AB2+x2AB2+9x2
4. Substitute into the Expression:
- Substitute the expressions for AE2AC2 and AD2AC2 into the original expression:
8(AE2AC2)−5(AD2AC2)=8⋅AB2+4x2AB2+9x2−5⋅AB2+x2AB2+9x2
5. Combine the Terms:
- Combine the fractions:
=8(AB2+4x2)−5(AB2+x2)AB2+9x2
- Simplifying the numerator:
=8AB2+32x2−5AB2−5x2AB2+9x2=(8−5)AB2+(32−5)x2AB2+9x2
=3AB2+27x2AB2+9x2
6. Factor Out Common Terms:
- Factor out 3 from the numerator:
=3(AB2+9x2)AB2+9x2=3
Final Answer:
Thus, the value of 8(AEAC)2−5(ADAC)2 is 3.
- Let BC be trisected by points D and E. This means BD=DE=EC.
- Let BD=DE=EC=x. Therefore, BC=3x.
- In triangle ABD:
AD2=AB2+BD2=AB2+x2(Equation 1)
- In triangle ABE:
AE2=AB2+BE2=AB2+(BD+DE)2=AB2+(2x)2=AB2+4x2(Equation 2)
- In triangle ABC:
AC2=AB2+BC2=AB2+(3x)2=AB2+9x2(Equation 3)
- From Equations 2 and 3, we have:
AE2AC2=AB2+4x2AB2+9x2
- From Equations 1 and 3, we have:
AD2AC2=AB2+x2AB2+9x2
- Substitute the expressions for AE2AC2 and AD2AC2 into the original expression:
8(AE2AC2)−5(AD2AC2)=8⋅AB2+4x2AB2+9x2−5⋅AB2+x2AB2+9x2
- Combine the fractions:
=8(AB2+4x2)−5(AB2+x2)AB2+9x2
- Simplifying the numerator:
=8AB2+32x2−5AB2−5x2AB2+9x2=(8−5)AB2+(32−5)x2AB2+9x2
=3AB2+27x2AB2+9x2
- Factor out 3 from the numerator:
=3(AB2+9x2)AB2+9x2=3
Thus, the value of 8(AEAC)2−5(ADAC)2 is 3.
Topper's Solved these Questions
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIV)
Explore 90 Videos
- DISCOUNTBook:KIRAN PUBLICATIONChapter:DISCOUNTExercise:Test Yourself
Explore 10 Videos
- LCM AND HCF Book:KIRAN PUBLICATIONChapter:LCM AND HCF Exercise:Test Yourself
Explore 18 Videos
Similar Questions
AC is the diameter of a circumcircle of ΔABC. Chord ED is par allel to the diameter AC. If ∠CBE=50∘, then the measure of ∠DECis
View SolutionA merchant allows 5% discount on the marked price of an article to his customers. What price should he mark on an article the cost price of which is 712.50, so as to make a clear profit of 3313% on his outlay ?
View SolutionFind the HCF of 513, 1134 and 1215
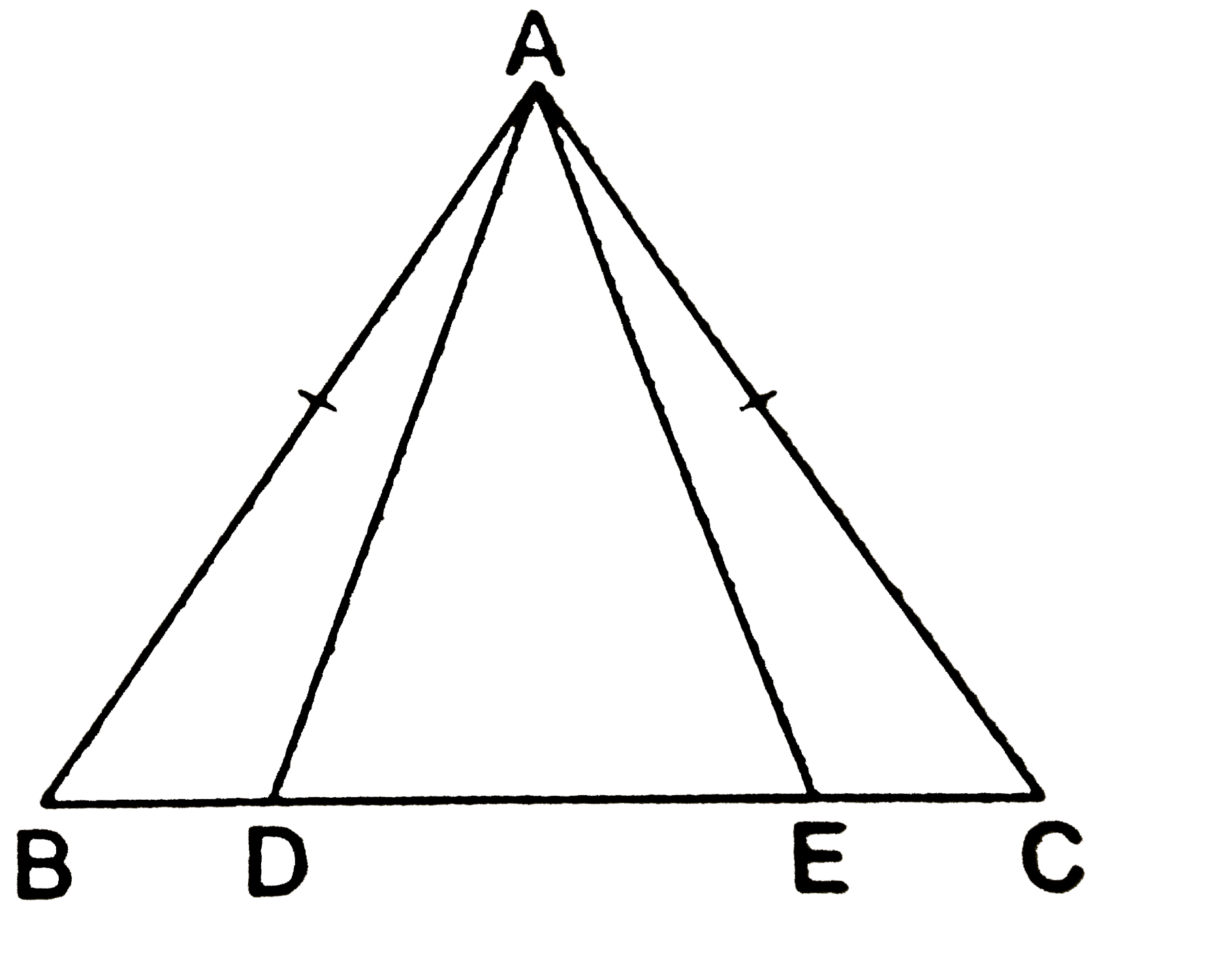
View SolutionIn an isosceles ΔABC with AB = AC, D and E are point on BC such that BE = CD. Show that AD = AE.
View Solution(a) ΔABC में , AB=5 सेमी , BC = 13 सेमी तथा AC = 12 सेमी है । यदि BC का मध्य बिंदु D है , तो माध्यिका AD कि माप ज्ञात कीजिए ।
(b) निम्न चित्र में ,ΔABC की माध्यिक AD=6 सेमी है । यदि आधार BC = 8 सेमी हो तो का AB2+AC2 मान ज्ञात कीजिए ।
View SolutionΔABC में DE||BC तथा AB और AC पर दो बिन्दु क्रमशः D और E है यदि ADAB=815 और EC =3.5 सेमी तो AE ज्ञात कीजिये
View SolutionIN ΔABC,BC2+AB2=AC2 then………..is the right angle.
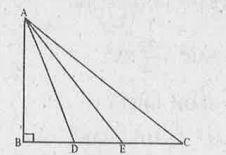
View Solutionఇచ్చిన పటంలో , ΔABC ఒక లంబకోణ త్రిభుజము. శీర్షము B వద్ద లంబకోణము కలదు. BC భుజాన్ని D మరియు E బిందువులు సమాత్రీఖండన చేస్తే అయిన 8AE2=3AC2+5AD2 అని చూపండి.
View SolutionΔABC में भुजाओं AB एवं AC क्रम दो बिन्दु D एवं E इस प्रकार ADDB=34 है कि एवं AC = 15 cm है। AE का मान ज्ञात करें।
View SolutionIn ΔABC, D and E are points on AB and AC respectively, such that DE∣∣BC. If ADDB=413 and AC = 20.4 cm, find AE.
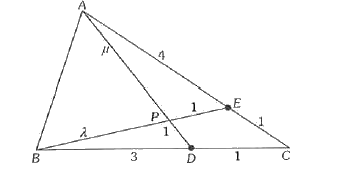
View SolutionΔABC में D तथा E क्रमश: BC तथा AC पर बिन्दु इस प्रकार हैं कि BD=3DC तथा AE=4EC रेखाओं AD तथा BE बिन्दु P पर प्रतिछेद करती है तब
View SolutionIn ΔABC,AD⊥BC, point D lies on BC. If AC2=CD⋅BD, prove that ∠BAC is a right angle.
View SolutionΔABC में, AB= AC बिंदु D भुजा BC इस प्रकार है, कि ∠BAD=50∘ और बिंदु E भुजा AC पर इस प्रकार है कि AE= AD तो ∠CDE का मान क्या होगा ?
View SolutionIn a ΔABC,AB=AC,D is a point on BC such that ∠BAD=50∘ and a point E on side AC such that AE = AD find ∠CDE.
View SolutionIn a ΔABC,AB=AC,D is a point BC such that ∠BAD=50∘ and a point E on side AC such that AE =AD find ∠CDE
View SolutionIn equilateral ΔABC. D is chosen on AC so that AD=13AC, and E is chosen on BC so that CE = 13BC. BD and AE intersect at F. Find the angle ∠CFB?
View Solution