In a LPP if the objective function Z= ax + by has the same maximum value on two comer points of the feasible region, then every point on the line segment joining these two points give the same .......... value. Solution in Punjabi
The correct Answer is:Maximum
Step by step video & text solution for In a LPP if the objective function Z= ax + by has the same maximum value on two comer points of the feasible region, then every point on the line segment joining these two points give the same .......... value. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023টপার এই প্রশ্নগুলো সমাধান করেছে
- LINEAR PROGRAMMING Book:ACCURATE PUBLICATIONChapter:LINEAR PROGRAMMING Exercise:QUESTIONS CARRYING 1 MARK (TYPE-III : TRUE OR FALSE QUESTIONS)
Explore 10 Videos
- LINEAR PROGRAMMING Book:ACCURATE PUBLICATIONChapter:LINEAR PROGRAMMING Exercise:QUESTIONS CARRYING 6 MARKS
Explore 7 Videos
- LINEAR PROGRAMMING Book:ACCURATE PUBLICATIONChapter:LINEAR PROGRAMMING Exercise:QUESTIONS CARRYING 1 MARK (TYPE-I : MULTIPLE CHOICE QUESTIONS)
Explore 15 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBook:ACCURATE PUBLICATIONChapter:INVERSE TRIGONOMETRIC FUNCTIONSExercise:QUESTIONS CARRYING 4 MARKS
Explore 27 Videos
- MATRICESBook:ACCURATE PUBLICATIONChapter:MATRICESExercise:QUESTIONS CARRYING 6 MARKS
Explore 4 Videos
সম্পর্কিত প্রশ্ন
If the feasible region for a linear programming problem is bounded, then the objective function Z = ax+by has both a maximum and a minimum value on R.
View SolutionFind the maximum value of f = x+2 y subject to the constraints
2x+3y≤6
x+4y≤4
x,y≥0
View SolutionThe feasible solution for a LPP is shown in Fig. Let. Z = 3x - 4 y be the objective function. Minimum of Z occurs at
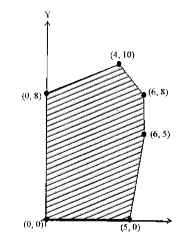
View SolutionWrite the value of tan−1[2sin(2cos−1√32)].
View SolutionIf A=⎡⎢⎣1−202130−21⎤⎥⎦,B=⎡⎢⎣72−6−21−3−425⎤⎥⎦ , find AB Also solve x−2y=10,2x+y+3z=8,−2y+z=7
View SolutionThe objective function Z=x1+x2 subject to x1+x2≤15,−2x1+3x2≤15,x1≤6,x2≥0 has maximum value of the feasible region (a) at only one point (b) at only two points (c) at every point of the segment joining two points (d) at every point of the line joining two points
View SolutionMaximum value of the objective function Z = ax +by in a LPP always occurs at only one corner point of the feasible region.
View SolutionIn a LPP, the maximum value of the objective function Z = ax +by is always 0, if origin is one of the corner point of the feasible region.
View SolutionWhich of the following statements is false? A) The feasible region is always a concave region B) The maximum (or minimum) solution of the objective function occurs at the vertex of the feasible region C) If two corner points produce the same maximum (or minimum) value of the objective function, then every point on the line segment joining these points will also give the same maximum (or minimum) two. values D) All of the above
View SolutionConsider the following statements
I. If the feasible region of an LPP is undbounded then maximum or minimum value of the obJective function Z = ax + by may or may not exist .
II. Maximum value of the objective function Z = ax + by in an LPP always occurs at only one corner point of the feasible region.
Ill. In an LPP, the minimum value of the objective function Z = ax + by is always 0, if origin is one of the corner point of the feasible region.
IV. In an LPP, the maximum value of the objective function Z = ax + by is always finite.
Which of the following statements are true?
View Solutionकिसी LPP में,यदि उद्देश्य फलन Z=ax+by का सुसंगत क्षेत्र के दो कोणीय बिन्दुओं पर समान अधिकतम मान हो, तो इन बिन्दुओं को मिलाने वाले रेखाखण्ड के सभी बिन्दुओं पर समान ..... मान प्राप्त होता है |
View Solutionकिसी LPP के उद्देश्य फलन Z=ax+by का अधिकतम मान सदैव सुसंगत क्षेत्र के केवल एक कोणीय बिन्दु पर प्राप्त होता है |
View Solutionकिसी LPP के उद्देश्य फलन Z=ax+by का न्यूनतम मान सदैव 0 होता है | यदि मूल बिन्दु उसके सुसंगत क्षेत्र का एक कोणीय बिन्दु है |
View SolutionMaximum value of the objective function Z = ax +by in a LPP always occurs at only one corner point of the feasible region.
View SolutionIn a LPP, the maximum value of the objective function Z = ax +by is always 0, if origin is one of the corner point of the feasible region.
View SolutionMaximum value of the objective function Z = ax + by in a LPP always occurs at only one corner point of the feasible region.
View Solution
