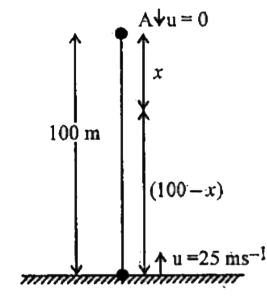
A stone is allowed to all from the top of a tower 100 m high and at the same time another stone is projected vertically upwards from the ground with a velocity of 25m/s. Calculate when and where the two stones will meet.
Suppose the two stones meet after t seconds at a distance of x metres from top of the tower.
For the downward motion of the stone allowed to fall from the top of the tower
u=0
a=+g=9.8ms−2
s=x
t=t
Using S=ut+12at2 we get
x=0×t+12×9.8t2
or x=4.9t2 ... 1
For the upward motion of the stone projected verticaly upwards
u=25ms−1
a=−g=−9.8ms−2
S=(100−x)m
t=t
Using S=ut+12at2 we get
100−x=25×t+12(−9.8)t2
or 100−x=25t−4.9t2 ........2
Putting the value of x from equation (1) in equation 2 we get
100−4.9t2=25t−4.9t2
or 100=25t
t=4s
Putting t=4 in equation 1 we get
x=4.9(4)2 m
=78.4m
∴ The two stones will meet each other after 4 seconds at a distnce of 78.4 m from the topof the tower.
Similar Questions
A stone is allowed to fall from the top of a tower 100m high and at the same time another stone is projected vertically upwards from the ground with a velocity of 25m/s. Calculate when and where the two stone will meet.
View Solution
A stone is allowed to fall from the top of a tower 300 m height and at the same time another stone is projected vertically up from the ground with a velocity 100m/s. Find when and where the two stones meet?
View Solution
Knowledge Check
A stone is dropped from the top of a 400m high tower. At the same time another stone is projected vertically upwards from the ground with a speed of 50m/s. The two stones will cross each other after a time
A2 sB4 sC6 sD8 s
A stone is dropped from the top of a tower 200 m high. At the same time, another stone is projected vertically upwards from the ground with a velocity of 40m/s. Calcuate when and where the two stones will mest.
View SolutionA stone is allowed to fall from the top of a tower 300 m height and at the same time another stone is projected vertically up from the ground with a velocity 100ms−1 . Find when and where the two stones meet ?
View SolutionForm the top of a tower 100m in height a ball is dropped and at the same time another ball is projected vertically upwards from the ground with a velcoity of 25ms−1. Find when and where the two balls will meet.
View SolutionA stone is dropped from a height 300 m and at the same time another stone is projected vertically upwards with a velocity of 100m/sec. Find when and where the two stones meet.
View SolutionFrom the top of a tower 100 m in height a ball is dropped and at the same time another ball is projected vertically upwards from the ground with a velocity of 25 m/s. Find when and where the two balls will meet? (g=9.8m/s)
View SolutionA ball A is dropped from the top of a tower 500m high and at the same instant another ball b is projected upwards with the velocity of 100m/s. after how much time and where the two balls will meet?
View SolutionA stone is dropped from a tower of height 200 m and at the same time another stone is projected vertically up at 50 m/s. The height at which they meet ? [g=10m/s2]
View Solution
