The entropy of any system is given by
S=α2β In [μkRJβ2+3]
where αandβ are the constants. μ,J,kandR are no. of moles, mechanical equivalent of heat, Boltzmann constant and gas constant respectively.
[Take S=dQT]
Choose the incorrect option from the following :
αandJ have the same dimensions.
S,β,kandμR have the same dimensions.
Sandα have different dimensions.
αandk have the same dimensions.
To solve the problem, we need to analyze the given expression for entropy S and determine the dimensions of the involved quantities. The expression is:
S=α2βln(μkRJβ2+3)
where α and β are constants, and μ,J,k,R are the number of moles, mechanical equivalent of heat, Boltzmann constant, and gas constant respectively.
Step 1: Analyze the logarithm argument
The argument of the logarithm must be dimensionless. Thus, we have:
μkRJβ2+3
Since 3 is dimensionless, the term μkRJβ2 must also be dimensionless.
Step 2: Determine the dimensions of each variable
1. Number of moles (μ): Dimensionless.
2. Mechanical equivalent of heat (J): Dimensionless.
3. Boltzmann constant (k): The dimension of k is energy per temperature, which can be expressed as:
(k)=ML2T−2K=ML2T−2K−1
4. Gas constant (R): The dimension of R is also energy per mole per temperature:
(R)=ML2T−2mol⋅K=ML2T−2K−1
Step 3: Analyze β
Since μkRJβ2 is dimensionless, we can write:
(kR)=(k)(R)=(ML2T−2K−1)(ML2T−2K−1)=M2L4T−4K−2
Thus, we have:
β2=kRJ⟹(β2)=(kR)=M2L4T−4K−2
This means:
(β)=√M2L4T−4K−2=ML2T−2K−1
Step 4: Analyze S
The dimension of entropy S is given by:
S=dQT
where dQ has the dimension of energy ML2T−2 and T has the dimension of temperature K:
(S)=ML2T−2K=ML2T−2K−1
Step 5: Analyze α
From the expression S=α2β, we have:
(α2β)=(S)
Thus,
(α2)(β)=ML2T−2K−1
Since (β)=ML2T−2K−1:
(α2)=ML2T−2K−1ML2T−2K−1=1⟹(α)=1
Step 6: Compare dimensions of variables
1. S has dimensions ML2T−2K−1.
2. α is dimensionless.
3. β has dimensions ML2T−2K−1.
4. k and R have dimensions ML2T−2K−1.
5. J and μ are dimensionless.
Conclusion: Identify the incorrect option
Now, we can analyze the options based on the dimensions we have calculated:
- Option 1: S and β have the same dimension - Correct.
- Option 2: S and α have different dimensions - Correct.
- Option 3: α and k have the same dimension - Incorrect (as α is dimensionless and k is not).
- Option 4: α and J have the same dimension - Correct (both are dimensionless).
Thus, the incorrect option is Option 3.
2. Mechanical equivalent of heat (J): Dimensionless.
3. Boltzmann constant (k): The dimension of k is energy per temperature, which can be expressed as:
(k)=ML2T−2K=ML2T−2K−1
4. Gas constant (R): The dimension of R is also energy per mole per temperature:
(R)=ML2T−2mol⋅K=ML2T−2K−1
2. α is dimensionless.
3. β has dimensions ML2T−2K−1.
4. k and R have dimensions ML2T−2K−1.
5. J and μ are dimensionless.
- Option 2: S and α have different dimensions - Correct.
- Option 3: α and k have the same dimension - Incorrect (as α is dimensionless and k is not).
- Option 4: α and J have the same dimension - Correct (both are dimensionless).
Topper's Solved these Questions
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - PHYSICS (SECTION-B)
40 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - PHYSICS (SECTION - A)
40 Videos
- JEE MAINS 2020BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2020EXERCISE - PHYSICS
246 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -B)
10 Videos
Similar Questions
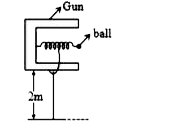
In a spring gun having spring constant 100 N/m a small ball 'B' of mass 100 g is put in its barrel (as shown in figure) by compressing the spring through 0.05 m. There should be a box placed at a distance 'd' on the ground so that the ball falls in it. If the ball leaves the gun horizontally at a height of 2 m above the ground. The value of d is ____ m. (g=10 m/s2)
View SolutionFor a gas CP−CV=R in a state P and CP−CV=1.10R in a state Q, TP and TQ are the temperatures in two different states P and Q respectively. Then
View SolutionFundamental frequency of two identical strings x and y are 450Hz and 300Hz resp. then find the ratio of tension in string x and y will be
View SolutionA mass of 10kg is suspended vertically by a rope of length 5 m from the roof. A force of 30 N is applied at the middle point of rope in horizontal direction .The angle made by upper half of the rope with vertical is θ=tan−1(x×10−1). The value of x is _______
(Given , g =10m/s2)
View SolutionIf |(1+beta^2,beta,beta^2),(3, alpha -2,3),(alpha,1,alpha)|=|(a1+alpha^2,1,beta),(alpha,beta-2,3),(alpha^2,1,beta)|=0 where alpha, beta in R and alpha lt beta then identify whichof the following statement(s) is(are) correct?
View SolutionPressure depends on distance as, P=αβexp(−αzkθ), where α,β are constants, z is distance, k is Boltzmann's constant and θ is temperature. The dimensions of β are :
View SolutionThe force of interaction between two atoms is given by F=αβexp(−x2αkt) , where x is the distance ,k is the Boltzmann constant and T is temperature and α and β are two constans. The dimension of β is :
View Solutionदूरी z के साथ दाब P का विचरण, P=αβe−az/kθ से व्यक्त किया जाता है, जहाँ α,β नियतांक हैं, k बोल्ट्समान नियतांक तथा θ ताप है । β का विमीय सूत्र होगा :
View SolutionThe temperature (T) of one mole of an ideal gas varies with its volume (V) as T= - alpha V^(3) + beta V^(2) , where alpha and beta are positive constants. The maximum pressure of gas during this process is
View Solutionα,βలు x2+5x+k బహుపది యొక్క శూన్యలు మరియు α−β=3 అయిన k విలువ
View SolutionPressure depends on distance as P=αβexp(−αzkθ) where αβ are constants z is distance k is Boltzmann is constant and θ is temperature. The dimension of β are
View SolutionPressure depends on distance as P=αβexp(−αzkθ) where αβ are constants z is distance k is Boltzmann is constant and θ is temperature. The dimension of β are
View SolutionThe force of interaction between two atoms is given by F=αβexp(−x2αkt) , where x is the distance ,k is the Boltzmann constant and T is temperature and α and β are two constans. The dimension of β is :
View SolutionPressure depends on distance as P=αβexp(−αzkθ) where αβ are constants z is distance k is Boltzmann is constant and θ is temperature. The dimension of β are
View SolutionPressure depends on distance as, P = alpha/beta exp (-(alpha z)/(k theta)) where alpha, beta are constants, z is distance, 'k' is Boltzmann's constant and theta is temperature. The dimension of beta are
View SolutionThe relation between time and displacement x is t=αx2+βx, where α and β are constants. (Take α=2m−2s,β=1m−1s)
View Solution

