In a quadrilateral ABCD∠A+∠C is 2 times ∠B+∠D. If ∠A=140∘∠D=60∘, then ∠B=
60∘
80∘
120∘
None of these
The correct Answer is:A
To solve the problem step by step, we will use the information given in the question.
Step 1: Write down the equations based on the information provided.
We know that:
1. ∠A+∠C=2(∠B+∠D)
2. The sum of angles in a quadrilateral is 360∘: ∠A+∠B+∠C+∠D=360∘
Step 2: Substitute the known values into the equations.
Given:
- ∠A=140∘
- ∠D=60∘
Substituting these values into the second equation:
140∘+∠B+∠C+60∘=360∘
This simplifies to:
∠B+∠C+200∘=360∘
Subtracting 200∘ from both sides gives:
∠B+∠C=160∘(Equation 1)
Step 3: Substitute into the first equation.
Now substitute ∠A and ∠D into the first equation:
140∘+∠C=2(∠B+60∘)
This simplifies to:
140∘+∠C=2∠B+120∘
Rearranging gives:
∠C=2∠B+120∘−140∘
Thus:
∠C=2∠B−20∘(Equation 2)
Step 4: Solve the equations simultaneously.
Now we have two equations:
1. ∠B+∠C=160∘ (Equation 1)
2. ∠C=2∠B−20∘ (Equation 2)
Substituting Equation 2 into Equation 1:
∠B+(2∠B−20∘)=160∘
This simplifies to:
3∠B−20∘=160∘
Adding 20∘ to both sides gives:
3∠B=180∘
Dividing by 3:
∠B=60∘
Step 5: Conclusion
Thus, the value of ∠B is 60∘.
We know that:
1. ∠A+∠C=2(∠B+∠D)
2. The sum of angles in a quadrilateral is 360∘: ∠A+∠B+∠C+∠D=360∘
Given:
- ∠A=140∘
- ∠D=60∘
140∘+∠B+∠C+60∘=360∘
This simplifies to:
∠B+∠C+200∘=360∘
Subtracting 200∘ from both sides gives:
∠B+∠C=160∘(Equation 1)
Now substitute ∠A and ∠D into the first equation:
140∘+∠C=2(∠B+60∘)
This simplifies to:
140∘+∠C=2∠B+120∘
Rearranging gives:
∠C=2∠B+120∘−140∘
Thus:
∠C=2∠B−20∘(Equation 2)
Now we have two equations:
1. ∠B+∠C=160∘ (Equation 1)
2. ∠C=2∠B−20∘ (Equation 2)
∠B+(2∠B−20∘)=160∘
This simplifies to:
3∠B−20∘=160∘
Adding 20∘ to both sides gives:
3∠B=180∘
Dividing by 3:
∠B=60∘
Thus, the value of ∠B is 60∘.
Topper's Solved these Questions
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - EXERCISE (Multiple Choice Questions) (LEVEL-2 )
15 Videos
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - EXERCISE (Match the Following)
2 Videos
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - NCERT SECTION (Exercise 8.2 )
11 Videos
- PROBABILITYBOOK - MTG IIT JEE FOUNDATIONCHAPTER - PROBABILITYEXERCISE - OLYMPIAD/HOTS CORNER
20 Videos
- STATISTICSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - Olympiad/HOTS Corner
20 Videos
Similar Questions
In the given figure, ABCD is a parallelogram, then ∠DBAand∠BDA are respectively equal to

View SolutionMatch the following:
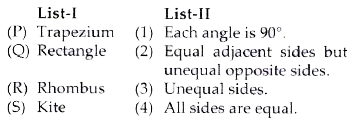
View SolutionABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA. AC is a diagonal. Show that :(i) SR ∣∣ ACand SR=12AC(ii) PQ = SR(iii) PQRS is a parallelogram
View SolutionA bag contains 8 red and 4_ green balls. One ball is selected at random. Find the probability that the ball drawn is red.
View SolutionThe weight (in kg) of 50 students are given below
40 45 55 62 50 51 56 69 61 36
60 56 69 38 35 63 57 50 57 48
40 63 53 64 47 42 56 51 42 60
55 39 64 57 64 44 66 35 59 59
73 62 49 63 37 63 54 72 44 60
Find the mean, median and mode respectively for the given data.
View Solutionकिसी चक्रीय चतुर्भुज ABCD में ∠A+∠B+∠C+∠D=?
View Solution∠A+12∠B+∠C=140∘, then ∠B is ∠A+12∠B+∠C=140∘, हे, तब ∠B हे।
View SolutionIf bisectors of ∠Aand∠B of a quadrilateral ABCD intersect each other at P, of ∠Band∠C at Q, of ∠Cand∠D at R and of ∠Dand∠A at S, then PQRS is a
View SolutionABCD is a parallelogram . If ∠A+∠C=120∘, then ∠B+∠D=________
View SolutionIn a ΔABC,∠A+∠B=65∘and∠B+∠C=140∘. Find the angles.
View Solutionयदि किसी चतुर्भुजABCD में ∠A+∠C=2(∠B+∠D) हो तथा ∠A=140∘, ∠D=60, हो तो ∠B=
View SolutionIn the parallelogram ABCD , ∠B−∠C=60∘.Find∠Aand∠D
View SolutionIn a rhombus ABCD, if ∠A=60∘ find ∠B,∠C&∠D.
View SolutionIf DeltaABC In, angleB+angleC=140^(@) And angleA+angleB=65^(@) If so angleA, angleB And angleC Find the value of.
View Solutionकिसी चतुर्भुज ABCD में ∠A=120∘ और ∠B=∠C=∠D तो ∠B का मान ज्ञात करे।
View Solution
