An isosceles triangle has a 10 inches base and two 13 inches sides .What other value can the base have and still yields a triangle with the same areas ?
18 inches
19 inches
24 inches
27 inches
The correct Answer is:C
To solve the problem of finding another base for the isosceles triangle that yields the same area, we can follow these steps:
Step 1: Calculate the height of the original triangle
We have an isosceles triangle with a base of 10 inches and two equal sides of 13 inches. To find the height, we can drop a perpendicular from the apex to the midpoint of the base. This creates two right triangles.
- The base of each right triangle is 102=5 inches.
- The hypotenuse (the equal sides) is 13 inches.
Using the Pythagorean theorem:
h2+52=132
h2+25=169
h2=169−25=144
h=√144=12 inches
Step 2: Calculate the area of the original triangle
The area A of a triangle is given by:
A=12×base×height
For our triangle:
A=12×10×12=60 square inches
Step 3: Set up the equation for the new triangle
Let the new base be 2y (since it is still an isosceles triangle with equal sides of 13 inches). The height remains the same at h.
Using the area formula again:
A=12×2y×h
Setting this equal to the area of the original triangle:
12×2y×12=60
This simplifies to:
12y=60
y=5
Step 4: Calculate the new base
The new base b is:
b=2y=2×5=10 inches
Step 5: Find the other possible base
To find another base that yields the same area, we can use the Pythagorean theorem again for the new triangle:
h2+y2=132
Substituting h=12:
122+y2=169
144+y2=169
y2=169−144=25
y=5
Now, we can find the new base:
New base=2y=2×5=10 inches
However, we also need to consider the possibility of a larger base that still maintains the same area. We can set up the equation:
12×2y×h=60
And solve for y again, leading to:
y4−169y2+3600=0
This can be factored or solved using the quadratic formula, yielding:
y=12 or 5
Thus, the new base can be:
b=2y=2×12=24 inches
Final Answer
The other possible base for the triangle that yields the same area is 24 inches.
We have an isosceles triangle with a base of 10 inches and two equal sides of 13 inches. To find the height, we can drop a perpendicular from the apex to the midpoint of the base. This creates two right triangles.
- The hypotenuse (the equal sides) is 13 inches.
h2+52=132
h2+25=169
h2=169−25=144
h=√144=12 inches
The area A of a triangle is given by:
A=12×base×height
For our triangle:
A=12×10×12=60 square inches
Let the new base be 2y (since it is still an isosceles triangle with equal sides of 13 inches). The height remains the same at h.
A=12×2y×h
Setting this equal to the area of the original triangle:
12×2y×12=60
This simplifies to:
12y=60
y=5
The new base b is:
b=2y=2×5=10 inches
To find another base that yields the same area, we can use the Pythagorean theorem again for the new triangle:
h2+y2=132
Substituting h=12:
122+y2=169
144+y2=169
y2=169−144=25
y=5
New base=2y=2×5=10 inches
12×2y×h=60
And solve for y again, leading to:
y4−169y2+3600=0
This can be factored or solved using the quadratic formula, yielding:
y=12 or 5
Thus, the new base can be:
b=2y=2×12=24 inches
The other possible base for the triangle that yields the same area is 24 inches.
Topper's Solved these Questions
- TRIANGLES Book:MTG IIT JEE FOUNDATIONChapter:TRIANGLES Exercise: Exercise (Multiple Choice Questions) (LEVEL -2)
Explore 15 Videos
- TRIANGLES Book:MTG IIT JEE FOUNDATIONChapter:TRIANGLES Exercise: Exercise (Match the following )
Explore 3 Videos
- TRIANGLES Book:MTG IIT JEE FOUNDATIONChapter:TRIANGLES Exercise:NCERT Section Exercise 6 .6
Explore 12 Videos
- SURFACE AREAS AND VOLUMESBook:MTG IIT JEE FOUNDATIONChapter:SURFACE AREAS AND VOLUMESExercise:OLYMPIAD/HOTS CORNER
Explore 20 Videos
Similar Questions
In a ΔABC , point D is on side AB and point E is on side Ac , such that BCED is a trapezium . If DE : BC = 3 : 5 , then area (ΔADE): area (ΔBCED)=
View SolutionList -I and List -II are given as options (a) , (b) , (c ) and (d) out of which one is correct .

View SolutionIn the figure , PS is the bisector of ∠QPR of ΔPQR . Prove that QSSR=PQPR .

View SolutionKunal arranged some metal blocks at the bottom of a tank as seen in the figure below. Then he filled the 30 cm by 25 cm by 25 cm tank with water. If each block is 4 cm long, 3 cm wide and 5 cm tall, then how much water is needed to fill the tank to 80% of the tank's height?
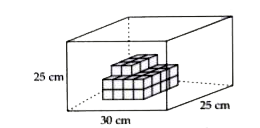
View SolutionFind the area of an isosceles triangle having the base x cm and one side y cm
View SolutionFind the area of an isosceles triangle having each of whose equal sides is 13 cm and whose base is 24 cm.
View SolutionEach of the equal sides of an isosceles triangle is 13 cm and its base is 24 cm. The area of the triangle is
View Solutionएक समद्विबाहु त्रिभुज का आधार 10 cm है और बराबर भुजाओं में से एक भुजा 13 cm हैं। त्रिभुज का क्षेत्रफल ज्ञात करें।
View Solution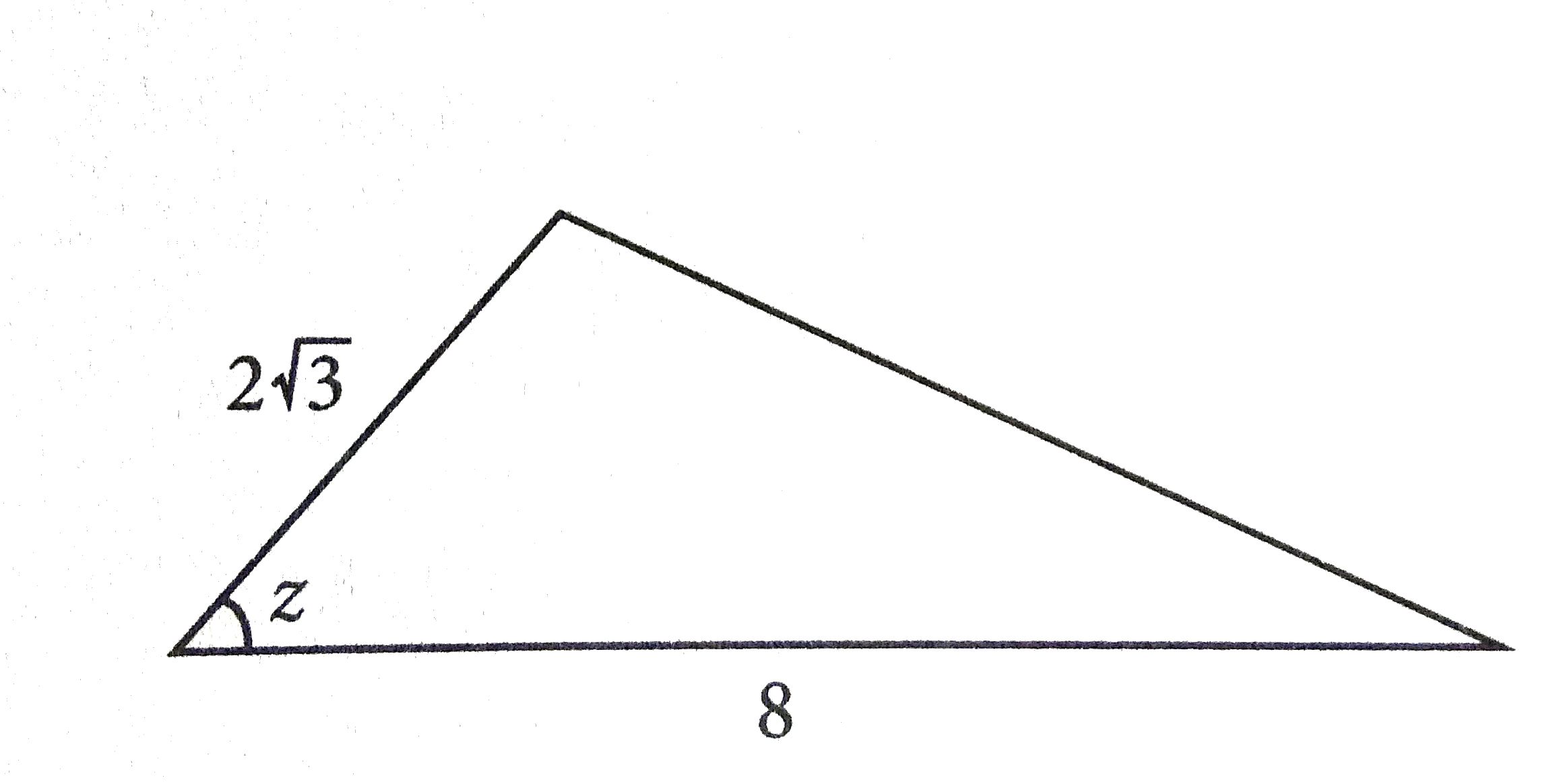
If the area of the triangle shown above is 12 squares inches, what is the value of cosz?
View Solutionसमद्विबाहु त्रिभुज की बराबर भुजाओ को एकही दिशा में बढ़ाने से आधार के नीचे जो कोण बनते है उनकी समद्विभाजक रेखाओ के मिलने से आधार के नीचे एक समद्विबाहु त्रिभुज बन जाता है, सिद्ध करे।
View SolutionThe lengths of two sides of a triangle are 50 inches and 63 inches. The angle opposite the 63-inch side is 66∘ . How many degrees are in largest angle of the triangle ?
View SolutionFor △ABC shown below, base ¯¯¯¯¯¯AC has a length of 16 inches and altitude ¯¯¯¯¯¯BD has a length of 8 inches. The area of a certain square is equal to the area of △ABC. What is the length, in inches, of a side of the square?
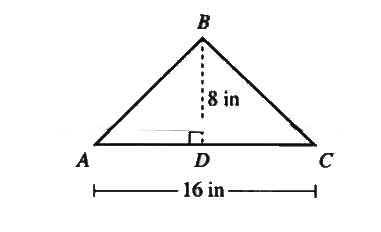
View SolutionA trapezoid has parallel bases that measure 3 inches and 9 inches and a height that measures 6 inches . What is the area, in square inches , of the trapezoid ?
View SolutionA right triangle has sides measuring 12 inches , 35 inches , and 37 inches . What is the cosine of the angle that lies opposite the 35-inch side ?
View SolutionFind the area of an isosceles triangle having the base xcm and one side ycm :
View Solution