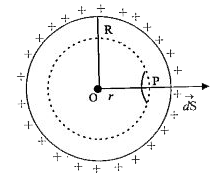
Using Gauss's Theorem, Derive an expression for electric field intensity due to uniformity charged hollow sphere : (c) At a point inside the shell
Electric field at point Inside the shell
Let P be the point inside the shell at a distance (r According to Gauss.s theorem
∮S→E.−→dS=qɛ0
Since, Gaussian surface contain no charge
i.r., q=0
∴ ∮S→E.−→dS=0ɛ0
∴ E=0
∴ There is no electric field intensity inside the hollow spherical shell.
Similar Questions
Knowledge Check
Intensity of electric field inside a uniformly charged hollow sphere is
AzeroBnon zero constantCchange with rDinversely proportional to r
Find expression for electric field intensity due to a uniformly charged thin spherical shell at a point outside the shell.
View SolutionDerive an expression for electric intensity E due to a uniformly charged thin spherical shell at a point outside the shell.
View SolutionUsing Gauss’s theorem in electrostatics, deduce an expression for electric field intensity due to a charged spherical shell at a point (i) inside (ii) on its surface (iii) outside it. Graphically show the variation of electric field intensity with distance from the centre of shell.
View SolutionApply Gauss's theorem to find an expression for the electric field intensity at a point due to a point charge.
View SolutionDerive an expression for the electric field intensity at a point outside a charged conducting sphere.
View SolutionState Gauss's theorem in electrostatics. Apply this theorem to derive an expression for electric field intensity at a point outside a uniformly charged thin spherical shell.
View Solution(a) Using Gauss's law, derive an expression for the electric field intensity at any point outside a uniformly charged thin spherical shell of radius R and charge density σC/m2. Draw the field lines when the charge density of the sphere is (i) positive, (ii) negative.
(b) A uniformly charged conducting sphere of 2.5 m in diameter has a surface charge density of 100 μC/m2. Calculate the
(i) charge on the sphere
(ii) total electric flux passing through the sphere.
View Solution

