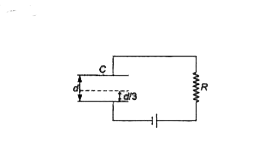
A parallel plate capacitor C with plates of unit area and separation d is filled with a liquid of dielectric constant K =2, the level of liquid is d3, intially, Suppose the liquid , level decreases at a constant speed v, the time constant as a function of time is
6ε0R5d+3υt
(15d+3υt)ε0R2d2−3dυ−9υ2t2
6εR5d−3υt
(15d−9υt)ε0R2d2+3υt−9υ2t2
The correct Answer is:A
We have time constant τ=RC
Now C.C1C2C1+C2=(Aε0d−x)(KAε0x)Aε0d−x+KAε0x=KAε0x+k(d−x) sincex=d3−vt
τ=RKAε0d3−vt+k(d−d3+vt) substitute A = 1, K = 2, τ=6Rε05d+3vt
Similar Questions
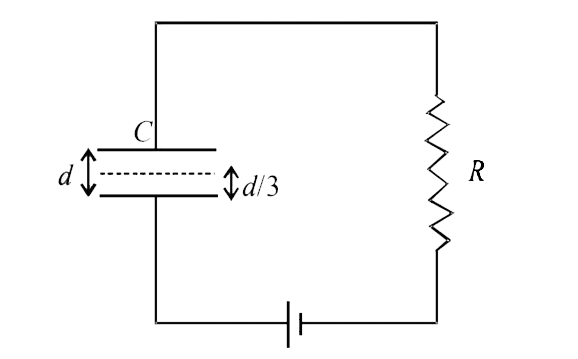
A parallel plate capacitor C with plates of unit area and separation d is filled with a liquid of dielectric constant K=2. The level of liquid is d/3 initially. Suppose the liquid level decreases at a constant speed v, the time constant as a function of time t is-
View SolutionA parallel plate capacitor, with plate area A and plate separation d, is filled with a dielectric slabe as shown. What is the capacitance of the arrangement ?
View Solution
Knowledge Check
A parallel plate capacitor C with plates of unit area and separation d is filled with a liquid of dielectric constant K=2. The level of liquid is d/3 initially. Suppose the liquid level decreases at a constant speed v, the time constant as a function of time t is-
 A6ε0R5d+3/tB(15d+9vt)ε0R2d3−3dvt−gv2t2C6ε0R5d−3vtD(15d−9vt)ε0R2d3+3dvt−9v2t2
A6ε0R5d+3/tB(15d+9vt)ε0R2d3−3dvt−gv2t2C6ε0R5d−3vtD(15d−9vt)ε0R2d3+3dvt−9v2t2A parallel plate capacitor C with plates of unit area and separation d is filled with a liquid of dielectric constant K=2. The level of liquid is d/3 initially. Suppose the liquid level decreases at a constant speed v, the time constant as a function of time t is-
 A(a) 6eπslon0R5d+3vtB(b) (15d+9vt)ε0R2d2−3dvt−9v2t2C(c) 6ε0R5d−3vtD(d) (15d−9vt)ε0R2d2−3dvt−9v2t2
A(a) 6eπslon0R5d+3vtB(b) (15d+9vt)ε0R2d2−3dvt−9v2t2C(c) 6ε0R5d−3vtD(d) (15d−9vt)ε0R2d2−3dvt−9v2t2A parallel plate capacitor of area ‘A’ plate separation ‘d’ is filled with two dielectrics as shown. What is the capacitance of the arrangement ?
 A3Kε0A4dB4Kε0A3dC(K+1)ε0A2dDK(K+3)ε0A2(K+1)d
A3Kε0A4dB4Kε0A3dC(K+1)ε0A2dDK(K+3)ε0A2(K+1)d
A capacitor of plate area A and separation d is filled with two dielectrics of dielectric constant K1=6andK2=4. New capacitance will be

View SolutionA parallel plate capacitor with plate area A & plate separation d is filled with a dielectric material of dielectric constant given byK=K0(1+αx).. Calculate capacitance of system: (given αd<<1).

View SolutionA parallel plate capacitor with plate area A & plate separation d is filled with a dielectric material of dielectric constant given byK=K0(1+αx).. Calculate capacitance of system: (given αd<<1).

View SolutionA capacitor of plate area A and separation d is filled with two dielectrics of dielectric constant K1=6andK2=4. New capacitance will be

View SolutionIf the gap between the plates of a parallel plate capacitor is filled with medium of dielectric constant k=2 , then the field between them
View Solution

