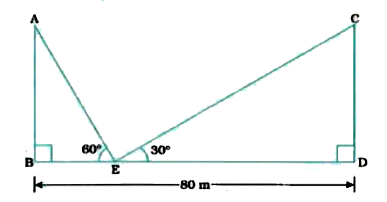
Two poles of equal height are standing opposite to each other on either side of a road which is 100 m wide .From a point between them on road , angle of elevation of their tops are 30∘and60∘ .The height of each pole (in metre ) is
25√3
20√3
28√3
30√3
The correct Answer is:A
To solve the problem step by step, we will use trigonometric principles and the information provided in the question.
Step 1: Understand the Setup
We have two poles of equal height (let's denote the height as h) standing on either side of a road that is 100 meters wide. We denote the points as follows:
- Let A and B be the tops of the poles.
- Let C be the point on the road where the angles of elevation are measured.
- The distance from point C to the base of pole A is x meters, and the distance from point C to the base of pole B is 100−x meters.
Step 2: Set Up the Trigonometric Relationships
From the point C:
1. The angle of elevation to the top of pole A is 30∘.
2. The angle of elevation to the top of pole B is 60∘.
Using the tangent function, we can write:
- For pole A:
tan(30∘)=hx
Since tan(30∘)=1√3, we have:
1√3=hx⟹h=x√3(1)
- For pole B:
tan(60∘)=h100−x
Since tan(60∘)=√3, we have:
√3=h100−x⟹h=√3(100−x)(2)
Step 3: Equate the Two Expressions for h
From equations (1) and (2), we can set them equal to each other:
x√3=√3(100−x)
Step 4: Solve for x
Cross-multiplying gives:
x=3(100−x)
x=300−3x
x+3x=300
4x=300⟹x=75 meters
Step 5: Substitute x Back to Find h
Now substitute x=75 back into either equation (1) or (2) to find h. Using equation (1):
h=75√3=25√3 meters
Conclusion
The height of each pole is 25√3 meters.
---
We have two poles of equal height (let's denote the height as h) standing on either side of a road that is 100 meters wide. We denote the points as follows:
- Let A and B be the tops of the poles.
- Let C be the point on the road where the angles of elevation are measured.
- The distance from point C to the base of pole A is x meters, and the distance from point C to the base of pole B is 100−x meters.
From the point C:
1. The angle of elevation to the top of pole A is 30∘.
2. The angle of elevation to the top of pole B is 60∘.
- For pole A:
tan(30∘)=hx
Since tan(30∘)=1√3, we have:
1√3=hx⟹h=x√3(1)
tan(60∘)=h100−x
Since tan(60∘)=√3, we have:
√3=h100−x⟹h=√3(100−x)(2)
From equations (1) and (2), we can set them equal to each other:
x√3=√3(100−x)
Cross-multiplying gives:
x=3(100−x)
x=300−3x
x+3x=300
4x=300⟹x=75 meters
Now substitute x=75 back into either equation (1) or (2) to find h. Using equation (1):
h=75√3=25√3 meters
The height of each pole is 25√3 meters.
Topper's Solved these Questions
- TRIGONOMETRY BOOK - KIRAN PUBLICATIONCHAPTER - TRIGONOMETRY EXERCISE - TYPE -IV
22 Videos
- TRIGONOMETRY BOOK - KIRAN PUBLICATIONCHAPTER - TRIGONOMETRY EXERCISE - TYPE -V
45 Videos
- TRIGONOMETRY BOOK - KIRAN PUBLICATIONCHAPTER - TRIGONOMETRY EXERCISE - TYPE - II
420 Videos
- TIME AND WORKBOOK - KIRAN PUBLICATIONCHAPTER - TIME AND WORKEXERCISE - TEST YOURSELF
25 Videos
Similar Questions
There are two vertical posts ,one on each side of a road ,just opposite to each other .One post is 108 metre high .From the top of this post , the angle of depression of the top and foot of the other post are 30∘and60∘ respectively .The height of the other post (in metre ) is
View SolutionA pole stands vertically ,inside a scalene triangular park ABC .If the angle of elevation of the top of the pole from each corner of tha park is same ,then in ΔABC , the foot of the pole is at the
View SolutionThe minimum value of 2sin2θ+3cos2θ is
View SolutionA contract to be completed in 56 days and 104 men were set towork each working 8 hours a day. After 30 days, 2/5th of the work is completed. How many additional men may be employed so that the work may be completed in time, each man now working 9 hours a day?
View SolutionTwo poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60∘and 30∘, respectively. Find the height of the poles and the distances of the point from the poles.
View SolutionTwo poles of equal heights are standing opposite to each other on either side of the road which is 80 m wide. From a point P between them on the road, the angle of elevation of the top of one pole is 60∘ and the angle of depression from the top of another pole is 30∘ find the height of pole and distances of the point P from the poles.
View SolutionTwo poles of equal height are standing opposite to each other on either side of the road, which is 80 m wide. From a point between then on the road, the angles of elevation of top of the poles are 60∘ and 30∘. Find the height of poles.
View SolutionTwo poles of equal heights are standing opposite each other on either side of the road, which is 80m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60∘ and 30∘, respectively . Find the height of the poles and the distances of the point from the poles.
View SolutionTwo poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60∘ to 30∘, respectively. Find the height of the poles and the distances of the point from the poles.
View SolutionTwo poles of equal heights are standing opposite to each other on either side of the road, which is 120 feet wide. From a point between them on the road, the angles of elevation of the top of the poles are 60∘ and 30∘ respectively. Find the height of the poles and the distances of the point from the poles.
View SolutionTwo poles of equal heights are standing opposite to each other on either side of the road, which is 120 feet wide. From a point between them on the road, the angles of elevation of the top of the poles are 60∘ and 30∘ respectively. Find the height of the poles and the distances of the point from the poles.
View SolutionTwo poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60∘and 30∘, respectively. Find the height of the poles and the distances of the point from the poles.
View SolutionTwo poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60∘and30∘, respectively. Find the height of the poles and the distances of the point from the poles.
View SolutionTwo poles of equal heights are standing opposite to each other on either side of the road which is 80 m wide. From a point between them on the road the angles of elevation of the top of the poles are 60∘ and 30∘ respectively. Find the height of the poles and the distances of the point from the poles.
View SolutionTwo poles of equal heights are standing opposite to each other on either side of the road, which is 120 feet wide. From a point between them on the road, the angles of elevation of the top of the poles are 60∘ and 30∘ respectively. Find the height of the poles and the distances of the point from the poles.
View SolutionTwo poles of equal heights are standing opposite each other on either side of the road, which is 80m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60∘and30∘, respectively. Find the height of the poles and the distances of the point from the poles.
View Solution
