If D, E and F are the mid-points of the sides of an equilateral triangle ABC, then the ratio of the area of triangle DEF and DCF is :
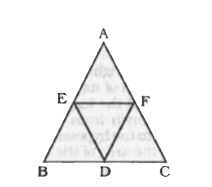
1.1:1
1:1.1
0.9:1
1:1
The correct Answer is:D
Step by step video solution for If D, E and F are the mid-points of the sides of an equilateral triangle ABC, then the ratio of the area of triangle DEF and DCF is : by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MENSURATIONBOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - TYPE - III
21 Videos
- MENSURATIONBOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - TYPE - IV
169 Videos
- MENSURATIONBOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - Test Yourself
28 Videos
- LCM AND HCF BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself
18 Videos
- MISCELLANEOUSBOOK - KIRAN PUBLICATIONCHAPTER - MISCELLANEOUSEXERCISE - TYPE-VI
15 Videos
Similar Questions
Knowledge Check
If D, E and F are the mid-points of sides BC, CA and AB respectively of △ABC, then the ratio of the areas of △DEF to the area of △ABC is :
A1:4B1:2C1:3D2:3D,E and F are the middle points of the sides of the triangle ABC, then
Acentroid of the triangle DEF is the same as that of ABCBorthocentre of the traiangl DRF is the circumcentre of ABCCorthocentre of the triangle DEF is the incentre of ABCDcentroid of the triangle DEF is not the same as that of ABCIf D, E and F are the mid points of BC, CA and AB respectively of the △ABC then the ratio of aria parallelogram DEFB and area of the trapezium CAFD is ,
A2:3B3:4C1:2D1:3
Three vertices of a triangle are A(1,2),B(−3,6)andC(5,4). If D, E and F are the mid-points of the sides opposite to the vertices A, B and C, respectively, show that the area of triangle ABC is four times the area of triangle DEF.
View SolutionD, E and F are respectively the mid-points of sides AB. BC and CA of △ABC. Find the ratio of the areas of △DEF and △ABC.
View Solutionlf D, E and F are respectively the midpoints of the sides BC, CA and AB of an equilateral triangle ABC, prove that △DEF is also an equilateral triangle.
View SolutionIn the given figure, ABCD is a rectangle; EandF are the mid-points of the sides BCandCD respectively. What is the ratio of the area of ΔAEF and that of ΔECF?
View SolutionABC is a triangle and D,E,F are the mid-points of the sides BC,CA, AB respectively . The ratio of the areas of ΔABCandΔDEF is :
View Solution
