A parallel plate capacitor has plate separation d and the area of each plate is A. The space between the plates is completely filled with a dielectric constant K. Derive the expression for the capacity of the parallel plate capacitor.
Parallel plate capacitor consists of two thin conducting plates each of area A held parallel to each other at a suitable, distance d. One of the plates is insulated and other is earthed. There is vacuum between the plates.
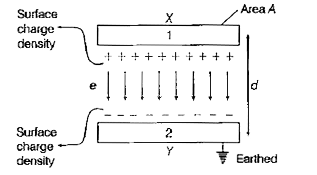
Suppose the plate X is given a charge of + q coulomb. By induction, ~q coulomb of charge is produced on the inner surface of the plate y and +q coulomb on the outer surface. Since, the plate Y is connected to the earth, the + q charge on the outer surface flows to the earth. Thus, the plates X and Y have equal and opposite charges.
Suppose the surface density of charge on each plate is σ. We know that the intensity of electric field at a point between two planes parallel sheets of equal and opposite charges is σ/ε0, where ε0 is the permittivity of free space. The intensity of electric field between the plates will be given by:
α=qA
and so, E=qε0A.......(i)
Now, let the potential difference between the two plates be V volt. Then, the electric field between the plates is given by
E=Vd
or V = Ed
On substituting the value of E from Eq. (i), we get
V=qdε0A
∴ Capacitance of the capacitor is given by
C=qV=qqd/ε0A or C=εAd
where, ε0=8.85×10−12F/m
Consider a dielectric inserted between the plates fully occupying the intervening region. The dielectric is polarised by the field with surface charge densities σ and −σP.
So, net electric field between the plates,
E=σ−σPε0
For linear dielectrics, we expect aP to be proportional to E0 i.e. to σ.
Thus, (σ−σP) is proportional to a and we can write,
σ−σP=σK
where, K is a constant of characteristic of the dielectric. Clearly,
K>1[σP<σ]
then, V=σdε0K=qdAε0K
∴ The capacitance C .with dielectric between the plates is given by
C=qV=ε0KAd
সম্পর্কিত প্রশ্ন
A parallel plate capacitor, with plate separation d and plate area A, has a capacitance of 5muF . Calculate the new capacitance if the plate separation is reduced to 0.75d and the capacitor is completely filled with dielectric of dielectric constant 8.
View SolutionA dielectric slab of thickness 't' is kept between the plates of a parallel plate capacitor separated by a distance 'd' (t<d) . Derive the expression for the capacity of the capacitor .
View SolutionDerive an expression for the capacitance of a parallel plate capacitor with dielectric as the medium between the plates.
View SolutionDefine the capacitance of capacitor. Derive an expression for the capacity of parallel plate capacitor with a dielectric slab placed in between the plates of capacitor.
View SolutionThe expression for the capacity of the capacitor formed by compound dielectric placed between the plates of a parallel plate capacitor as shown in figure, will be (area of plate = A )
View SolutionThe terminals of a battery of emf V are connected to the two plates of a parallel plate capacitor. If the space between the plates of the capacitor is filled with an insulator of dielectric constant K, then :
View SolutionA parallel plate capacitor has the space between its plates filled by two slabs ofthickness d2 each and dielectric constant k1andk2. d is the plate separation of the capacitor. The capacitance of the capacitor is :
View SolutionFind an expression for the capacitance of a parallel plate capacitor when a dielectric slab of dielectric constant K and thickness t=(d)/(2) but the same area on the plates is inserted between the the capacitors plate. (d=separation between the plates)
View Solution

