Find an expression for magnetic flux density at the centre of a circular coil carrying current.
Let us consider a circular loop of radius a with centre C. The plane of the coil be perpendicular to the plane of the paper and current I be flowing in the direction shown. Suppose P is any point on the axis at direction r from the centre.
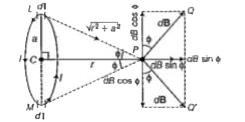
Now, consider a current element I dl on top (L). where current comes out of paper normally, whereas at bottom (M) enters into the plane paper normally.
LP⊥dl
Also, MP⊥dl
LP=MP=√r2+a2
The magnetic field at P due to current element Idl, according to Biot-Savart.s law is given by
dB=μ04π⋅Idlsin90∘(r2+a2)
where, a = radius of circular loop
and r= distance of point P from centre along the axis.
Net magnetic field,
B=∮dBsinϕ=∮μ04π(Idlr2+a2)⋅a√r2+a2
[∴sinϕ=a√r2+a2,inΔPCL]
=μ04πIa(r2+a2)3/2∮dl
B=μ04πIa(r2+a2)3/2(2πa) [∴dl=2πa]
or B=μ0la22(r2+a2)3/2 .......(i)
For N turns, B=μ0NIa22(r2+a2)3/2
The direction is along the axis and away from the loop, current in coil is anti-clockwise. Now putting, r = 0 in Eq. (i) as for centre, we get
B=μ0I2a.
Similar Questions
A current of 4A is flowing through a circular coil of radius 20 cm containing 200 turns. Find the magnetic flux density at the centre of the coil.
View SolutionState the expression for the magnetic field due to a circular are of wire carrying a current I. Hence find the magnetic field at the centre of circular coil and having n turns.
View SolutionObtain an expression for magnetic flux density B at the centre of a circular coil of radius R, having N turns and carrying a current I.
View SolutionCalculate magnetic flux density of the magnetic field at the centre of a circular coil of 50 turns, having radius of 0.5 m and carrying a current of 5A.
View SolutionObtain an expression for magnetic flux density B at the centre of a circular coil of radius R, having N turns and carrying a current I.
View SolutionIs the magnetic field at the centre of the current carrying circular coil parallel to the plane of the coil?
View SolutionFind the magnetic field induction at a point on the axis of a circular coil carrying current and hence find the magnetic field at the centre of circular coil carrying current.
View SolutionObtain an expression for magnetic induction at the centre of current carrying circular coil.
View Solution

