Apply Ampere's circuital law, find the magnetic flux density at the centre of a long solenoid carrying current.
Let us consider a solenoid having current I, number of turns per unit length n. To calculate the magnetic field B, we consider a loop PQRS having length L Hence, total current through the loop is (nL)I.
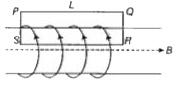
According to Ampere.s circuital law,
∫PQRSB⋅dl=μ0(NLl)
∮B⋅dl=∮QPB⋅dl+∫RQB⋅dl+∫SRB⋅dl+∫PSB⋅dl
Now ∫RQB⋅dl=∫PS⋅dl=0
(Because along QR and PS the field B is at right angles to d l, so that
B⋅dl=B⋅dlcos90∘=0)
∮B⋅dl=∫QP0dl+∫RQBdlcos90∘+∫SRBdlcos0∘+∫PSBdlcos90∘
=0+0+B∫SRdl+0=BL
Hence, from Ampere.s law,
∮B⋅dl=μ0× current enclosed by PQRSP
The current in each turns is I, so that current enclosed by the loop is nLl.
∴Inet=nLI
∮B⋅dl=μ0×nLI
∴BL=μ0nLI⇒B=μ0nI
Similar Questions
Find magnetic flux density at a point on the axis of a long solenoid having 5000 turns/m when it carrying a current of 2 A
View SolutionUsing Ampere's circuital law, find the magnetic flux density at the centre of a long solenoid carrying current.
View SolutionApplying Ampere's circuital law, find magnetic field due to toroidal solenoid.
View SolutionApplying Ampere's circuital law, find magnetic field due to a straight long solenoid.
View SolutionUsing Ampere's circuital law, derive an expression for the magnetic field along the axis of a toroidal solenoid.
View SolutionState and prove Ampere's Circuital Law for a circular path. Derive an expression for magnetic field due to a long current carrying wire.
View SolutionState and explain Ampere's circuital law and find magnetic field intensity at point well within the solenoid carrying current.
View SolutionWrite down the expression of magnetic flux density at the centre of a long solenoid carrying current.
View Solution

