Radii of two circles are respectively 25 cm and 9 cm and their centres are 34 cm apart common tangent to the two.
The correct Answer is:30 cm
To find the length of the common tangent to two circles with given radii and distance between their centers, we can follow these steps:
1. Identify the Given Values:
- Radius of the first circle (R) = 25 cm
- Radius of the second circle (r) = 9 cm
- Distance between the centers of the circles (d) = 34 cm
2. Use the Formula for the Length of the Direct Common Tangent:
The formula for the length of the direct common tangent (PQ) between two circles is given by:
PQ=√d2−(R−r)2
3. Substitute the Values into the Formula:
- First, calculate R−r:
R−r=25−9=16 cm
- Now substitute the values into the formula:
PQ=√342−(16)2
4. Calculate 342 and 162:
- 342=1156
- 162=256
5. Subtract 162 from 342:
1156−256=900
6. Take the Square Root:
PQ=√900=30 cm
Final Answer:
The length of the common tangent (PQ) is 30 cm.
---
- Radius of the first circle (R) = 25 cm
- Radius of the second circle (r) = 9 cm
- Distance between the centers of the circles (d) = 34 cm
The formula for the length of the direct common tangent (PQ) between two circles is given by:
PQ=√d2−(R−r)2
- First, calculate R−r:
R−r=25−9=16 cm
- Now substitute the values into the formula:
PQ=√342−(16)2
- 342=1156
- 162=256
1156−256=900
PQ=√900=30 cm
The length of the common tangent (PQ) is 30 cm.
Topper's Solved these Questions
- CIRCLE AND ITS TANGENT LINESBOOK - LUCENT PUBLICATIONCHAPTER - CIRCLE AND ITS TANGENT LINESEXERCISE - EXERCISE 8A
71 Videos
- CIRCLE AND ITS TANGENT LINESBOOK - LUCENT PUBLICATIONCHAPTER - CIRCLE AND ITS TANGENT LINESEXERCISE - EXERCISE 8B
27 Videos
- CENTRE OF TRIANGLEBOOK - LUCENT PUBLICATIONCHAPTER - CENTRE OF TRIANGLEEXERCISE - EXERCISE-6B
8 Videos
- CONGRUENCE AND SIMILAR TRIANGLES BOOK - LUCENT PUBLICATIONCHAPTER - CONGRUENCE AND SIMILAR TRIANGLES EXERCISE - EXERCISE-5B
8 Videos
Similar Questions
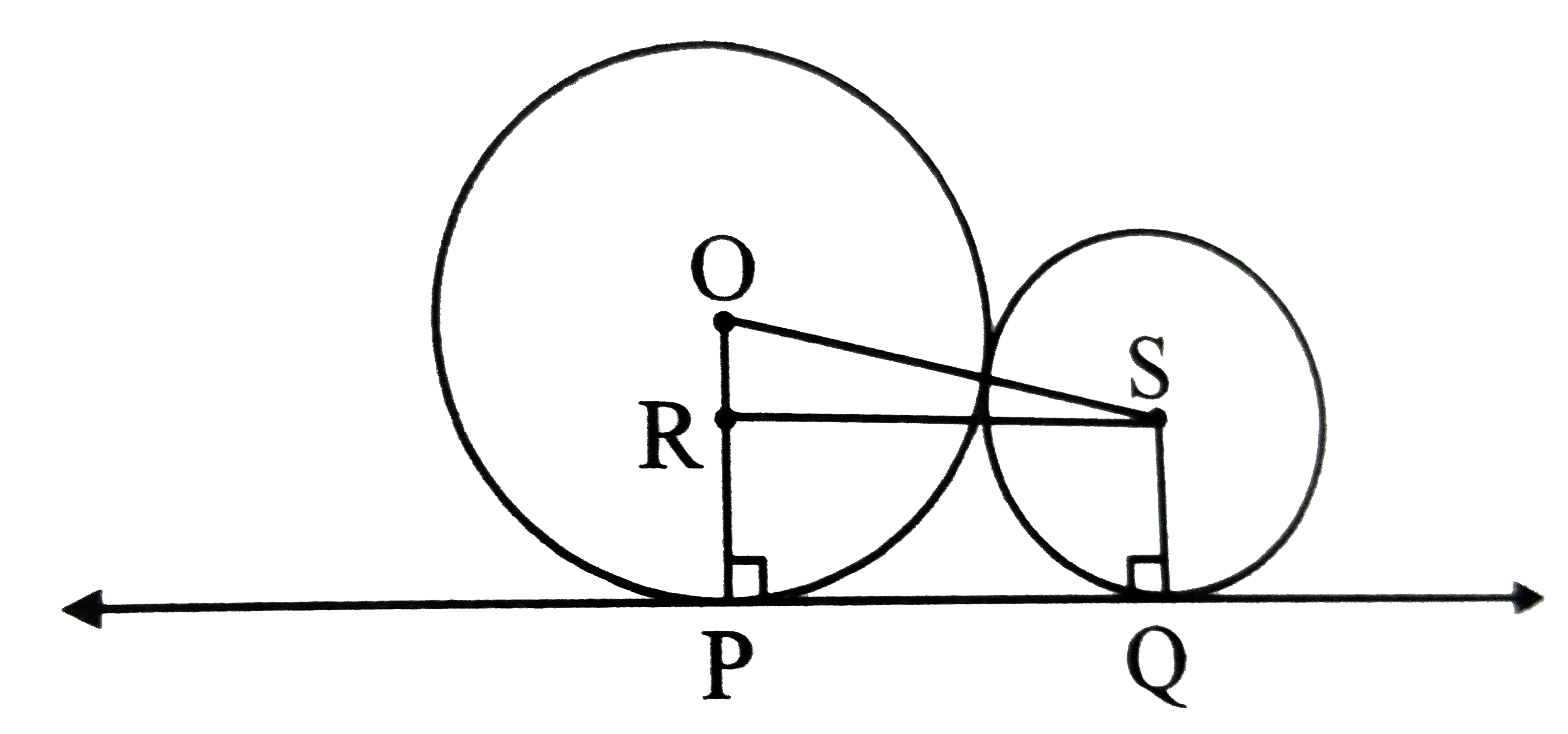
In the adjoining figure , line PQ is a common tangent to the externally touching circles and the radii of two circles are 25cm and 9cm. Find the length of the common tangent segment of these circles.
View SolutionThe distance between the centres of two circles having radii 8 cm and 3 cm, is 13 cm. The length (in cm) of the direct common tangent of the two circle is
View Solution
Knowledge Check
SR is dirrect common tangent of two circles whose radii are respectively 8 cm and 3 cm and centres are 13 cm apart. If S and R are points of contact, then the length of SR is
A17 cmB10 cmC12 cmD11 cmIf the radii of two circles be 6 cm and 3 cm and the length of the transverse common tangent be 8 cm, then the distance be tween the two centres is
A√145cmB√140cmC√150cmD√135cmIf the radii of two circles be 8 cm and 4 cm and the length of the transverse common tangent be 13 cm, then find the distance between the two centers is
A√313cmB√125 cmC5√2 cmD√135 cm
The distance between the centres of two circles having radii 9 cm and 4 cm is 13 cm. What is the length of the direct common tangent of these circles ?
View SolutionDraw two circle of radius 5 cm and 3 cm with their centres 9 cm apart. From the centre of each circle, draw tangents to other circles.
View SolutionTwo circles with radii 25 cm and 9 cm touch each other externally. The length of the direct common tangent is
View SolutionThe distance between the centres of two circles having radii 5 cm and 6 cm is 10 cm. Find the length (in cm) of direct common tangent.
View SolutionThe distance between the centre of two circles having radii 5 cm and 6 cm is √10 cm. find the length (in cm) of direct common tangent.
View Solution
