In a triangle ABC, ∠B=2∠C=2∠A. What is the ratio of AC to AB ?
√2:1
√3:1
1:1
1:√2
To solve the problem, we need to find the ratio of sides AC to AB in triangle ABC, given that ∠B=2∠C=2∠A.
1. Define the Angles:
Let ∠A=x. Then, according to the problem:
∠B=2xand∠C=x
2. Sum of Angles in a Triangle:
The sum of the angles in a triangle is 180∘:
∠A+∠B+∠C=180∘
Substituting the expressions for the angles:
x+2x+x=180∘
Simplifying this gives:
4x=180∘
Therefore:
x=45∘
3. Calculate Each Angle:
Now we can find each angle:
∠A=45∘,∠B=90∘,∠C=45∘
4. Identify the Type of Triangle:
Since ∠B=90∘, triangle ABC is a right triangle with:
∠A=45∘and∠C=45∘
This means triangle ABC is an isosceles right triangle.
5. Use Properties of Isosceles Right Triangle:
In an isosceles right triangle, the sides opposite the 45-degree angles are equal. Let:
AB=xandAC=x
The hypotenuse BC can be calculated using the Pythagorean theorem:
BC=√AB2+AC2=√x2+x2=√2x2=x√2
6. Find the Ratio of AC to AB:
Now we find the ratio of AC to AB:
Ratio=ACAB=x√2x=√2
7. Final Ratio:
Thus, the ratio of AC to AB is:
Ratio=√2:1
Conclusion:
The required ratio of AC to AB is √2:1.
Let ∠A=x. Then, according to the problem:
∠B=2xand∠C=x
The sum of the angles in a triangle is 180∘:
∠A+∠B+∠C=180∘
Substituting the expressions for the angles:
x+2x+x=180∘
Simplifying this gives:
4x=180∘
Therefore:
x=45∘
Now we can find each angle:
∠A=45∘,∠B=90∘,∠C=45∘
Since ∠B=90∘, triangle ABC is a right triangle with:
∠A=45∘and∠C=45∘
This means triangle ABC is an isosceles right triangle.
In an isosceles right triangle, the sides opposite the 45-degree angles are equal. Let:
AB=xandAC=x
The hypotenuse BC can be calculated using the Pythagorean theorem:
BC=√AB2+AC2=√x2+x2=√2x2=x√2
Now we find the ratio of AC to AB:
Ratio=ACAB=x√2x=√2
Thus, the ratio of AC to AB is:
Ratio=√2:1
The required ratio of AC to AB is √2:1.
Similar Questions
Knowledge Check
In a ΔABC,∠C=3∠B=2(∠A+∠B), then ∠B = ?
A20∘B40∘C60∘D80∘In △ABC ,AB=AC , ∠B=40∘ Then ∠C is equal to
A50∘B40∘C80∘D140∘In ΔABC, if ∠A:∠B:∠C=1:2:3, then what is BC : CA : AB ?
A1:2:3B1:√3:2C2:√3:1D√3:1:2
In a ΔABC,∠B=2∠C Angle bisector AD and BE intersect of O. AB = CD find ∠ABC
View SolutionIn a △ABC, If AB = AC and ∠A=70 Find ∠Band∠C
View SolutionIn ΔABC, If ∠C=3∠A,BC=27,andAB=48. Then the value of AC is ______
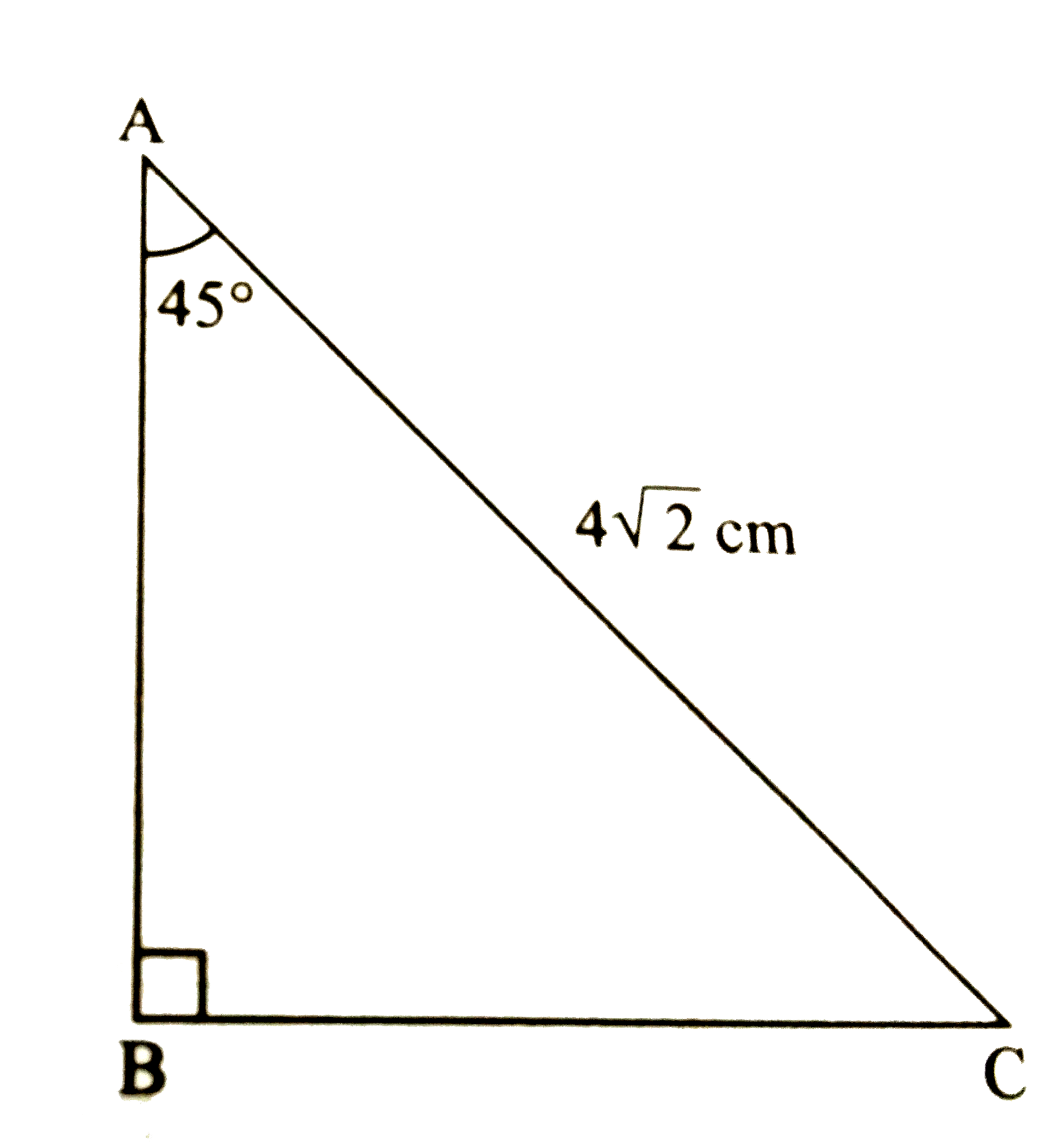
View SolutionIn △ABC,∠ABC=90∘
∠BAC=45∘ and AC =4√2cm,
then find AB.
View SolutionIn triangle ABC, angle B is right angled, AC=2 and A(2,2),B(1,3) then the length of the median AD is
View Solution
