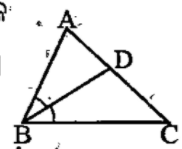
Let ABC be a right angled triangle with BC = 5 cm and AC = 12 cm. Let D be a point on the hypotenuse AB such that ∠BCD=30∘ . What is length of CD ?
6013cm
172 cm
1205+12√2 cm
1205+12√3 cm
To solve the problem, we will follow these steps:
Step 1: Identify the triangle and its sides
We have a right-angled triangle ABC where:
- BC = 5 cm (one leg)
- AC = 12 cm (the other leg)
Step 2: Use the Pythagorean theorem to find the hypotenuse AB
The Pythagorean theorem states that in a right-angled triangle, the square of the hypotenuse (AB) is equal to the sum of the squares of the other two sides (AC and BC).
AB2=AC2+BC2
AB2=122+52
AB2=144+25
AB2=169
AB=√169=13 cm
Step 3: Calculate the area of triangle ABC
The area of triangle ABC can be calculated using the formula:
Area=12×base×height
Here, we can take AC as the base and BC as the height:
AreaABC=12×AC×BC=12×12×5=30 cm2
Step 4: Set up the area equations for triangles BCD and ACD
Let CD = x. We can express the areas of triangles BCD and ACD.
For triangle BCD:
AreaBCD=12×BC×CD×sin(30∘)
Since sin(30∘)=12:
AreaBCD=12×5×x×12=5x4 cm2
For triangle ACD:
AreaACD=12×AC×CD×sin(60∘)
Since sin(60∘)=√32:
AreaACD=12×12×x×√32=3√3x cm2
Step 5: Set up the equation for the total area
The total area of triangle ABC is equal to the sum of the areas of triangles BCD and ACD:
AreaABC=AreaBCD+AreaACD
Substituting the areas we calculated:
30=5x4+3√3x
Step 6: Solve for x
To eliminate the fraction, multiply the entire equation by 4:
120=5x+12√3x
Combine like terms:
120=x(5+12√3)
Now solve for x:
x=1205+12√3
Step 7: Final answer
Thus, the length of CD is:
CD=1205+12√3 cm
We have a right-angled triangle ABC where:
- BC = 5 cm (one leg)
- AC = 12 cm (the other leg)
The Pythagorean theorem states that in a right-angled triangle, the square of the hypotenuse (AB) is equal to the sum of the squares of the other two sides (AC and BC).
AB2=122+52
AB2=144+25
AB2=169
AB=√169=13 cm
The area of triangle ABC can be calculated using the formula:
Area=12×base×height
Here, we can take AC as the base and BC as the height:
AreaABC=12×AC×BC=12×12×5=30 cm2
Let CD = x. We can express the areas of triangles BCD and ACD.
AreaBCD=12×BC×CD×sin(30∘)
Since sin(30∘)=12:
AreaBCD=12×5×x×12=5x4 cm2
AreaACD=12×AC×CD×sin(60∘)
Since sin(60∘)=√32:
AreaACD=12×12×x×√32=3√3x cm2
The total area of triangle ABC is equal to the sum of the areas of triangles BCD and ACD:
AreaABC=AreaBCD+AreaACD
Substituting the areas we calculated:
30=5x4+3√3x
To eliminate the fraction, multiply the entire equation by 4:
120=5x+12√3x
Combine like terms:
120=x(5+12√3)
Now solve for x:
x=1205+12√3
Thus, the length of CD is:
CD=1205+12√3 cm
Similar Questions
एक समकोण ΔABC,B पर इस प्रकार समकोणिक हैं कि AB = 12 सेमी तथा BC = 16 सेमी। बिंदु B से कर्ण AC पर लम्ब बनाया जाता हैं जोकि D पर मिलता हैं। लम्ब BD की लगभग लम्बाई हैं
View Solutionमान लीजिए कि एक समकोण त्रिभुज ABC है जहां BC = 3 सेमी. और AC = 4 सेमी. है। कर्ण AB पर एक बिंदु इस प्रकार है कि ∠BCD=30∘ है। CD की लंबाई क्या है?
View SolutionΔABC is a right angle triangle (right angled at B), BD is perpendicular to AC. If AC=16cmBC=9cm, find the length of CD.
View SolutionLet ABC be a right triangle with length of side AB=3 and hyotenus AC=5. If D is a point on BC such that BDDC=ABAC, then AD is equal to
View Solutionकिसी समकोण त्रिभुज ABC में, ∠B=90∘.
यदि AC=13cm, BC=5cm. है, तो AB ज्ञात कीजिएI
View SolutionIn a right-angled triangle ABC, if angle B=90°, BC = 3 cm and AC = 5 cm, then the length of side AB is
View Solution△ABCରେ ∠ABC ର ସମଦ୍ବିଖଣ୍ଡକ AC ବାହୁକୁ D ବିନ୍ଦୁରେ ଛେଦ କରେ AB=8ସେ.ମି., BC=12 ସେ.ମି. ଏବଂ AC = 10. ସେ.ମି. ହେଲେ CD. ବାହୁର ଦୈର୍ଘ୍ୟ କେତେ ସେ.ମି. ?
View SolutionLet ABC be a right triangle with length of side AB=3 and hyotenus AC=5. If D is a point on BC such that BDDC=ABAC, then AD is equal to
View Solution
