If v=√5000+24xms then calculate acceleration.
To find the acceleration when the velocity v is given as a function of displacement x, we can follow these steps:
1. Identify the given equation for velocity:
v=√5000+24x
2. Recall the relationship between acceleration, velocity, and displacement:
The acceleration a can be expressed as:
a=vdvdx
where dvdx is the derivative of velocity with respect to displacement.
3. Differentiate the velocity function with respect to x:
We need to find dvdx. Start by differentiating v:
v=(5000+24x)1/2
Using the chain rule:
dvdx=12(5000+24x)−1/2⋅(24)
Simplifying this gives:
dvdx=242√5000+24x=12√5000+24x
4. Substitute v and dvdx into the acceleration formula:
Now substitute v and dvdx into the formula for acceleration:
a=v⋅dvdx=√5000+24x⋅12√5000+24x
5. Simplify the expression:
The √5000+24x terms will cancel out:
a=12m/s2
Final Answer:
The acceleration is:
12m/s2
v=√5000+24x
The acceleration a can be expressed as:
a=vdvdx
where dvdx is the derivative of velocity with respect to displacement.
We need to find dvdx. Start by differentiating v:
v=(5000+24x)1/2
Using the chain rule:
dvdx=12(5000+24x)−1/2⋅(24)
Simplifying this gives:
dvdx=242√5000+24x=12√5000+24x
Now substitute v and dvdx into the formula for acceleration:
a=v⋅dvdx=√5000+24x⋅12√5000+24x
The √5000+24x terms will cancel out:
a=12m/s2
The acceleration is:
12m/s2
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
80 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
Knowledge Check
A body moving with some initial velocity and having uniform acceleration attains a final velocity v m/s after travelling x m. If its final velocity is v = √180−7x, find the acceleration of the body.
A−3.5m/s2B−7m/s2C−15m/s2D−30m/s2If the velocity of a particle is given by v=(180−16x)12ms, then its acceleration will be
AzeroB8ms2C−8ms2D4ms2For motion of an object along the x-axis the velocity v dipends on the displacement x an v=3x2, then what is the acceleration at x=2m.
A48ms−2B80ms−2m.C18ms−2D10ms−2
A wheel of radius R=1 m rolls on ground with uniform velocity v=2 m/s . Calculate the relative acceleration of topmost point of wheel with respect to bottom most point (in m/s2).
View SolutionA particle of mass m moves in a circle of radius R in such a way that its speed (v) varies with distance (s) as v=a√s where a is a constant. Calcualte the acceleration and force on the particle.
View SolutionThe velocity time relation of a particle is given by v =(3t2−2t−1)m/s Calculate the position and acceleration of the particle when velocity of the particle is zero . Given the initial position of the particle is 5m .
View SolutionThe motion of a body is given by the equation dv/dt=6−3v, where v is in m//s. If the body was at rest at t=0
(i) the terminal speed is 2m/s
(ii) the magnitude of the initial acceleration is 6m/s2
(iii) The speed varies with time as v=2(1−e−3t)m/s
(iv) The speed is 1m/s, when the acceleration is half initial value
View SolutionThe diagram shows variation of 1v with respect to time (where v is in m/s).
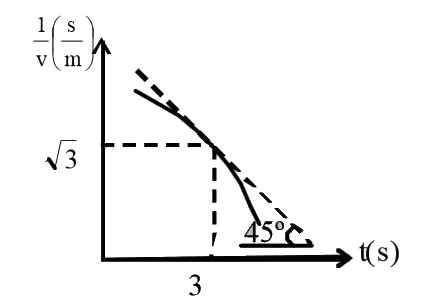
What is the instantaneous acceleration of body at t=3 sec. (inms2).
View Solution

