Consider the following statements :
1. Let D be a point on the side BC of a triangle ABC: If area of triangle ABD = area of triangle ACD, then for all points O on AD, area of triangle ABO = area of triangle ACO.
2. If G is the point of concurrence of the medians of a triangle ABC, then area of triangle ABG = area of triangle BCO = area of triangle ACG.
Which of the above statements is/are correct?
1 only
2 only
Both 1 and 2
Niether 1 nor 2
To solve the problem, we need to analyze both statements regarding the areas of triangles formed by certain points in triangle ABC.
Step 1: Analyze Statement 1
1. Understanding the statement: We have triangle ABC with point D on side BC. The statement claims that if the area of triangle ABD is equal to the area of triangle ACD, then for any point O on line AD, the area of triangle ABO will equal the area of triangle ACO.
2. Visualizing the scenario:
- Let the area of triangle ABD = Area of triangle ACD = k (some constant).
- Since D divides BC into two segments such that the areas of triangles ABD and ACD are equal, line AD bisects the area of triangle ABC.
3. Considering point O on AD:
- Any point O on line AD will create two smaller triangles, ABO and ACO.
- Since O lies on AD, the heights from O to line BC for both triangles ABO and ACO will be proportional to the segments AD is divided into by point O.
4. Conclusion for Statement 1:
- Since the areas of triangles ABO and ACO depend on the same base (line segment BC) and the heights from point A to line BC are equal, the areas of triangles ABO and ACO will also be equal.
- Therefore, Statement 1 is correct.
Step 2: Analyze Statement 2
1. Understanding the statement: The second statement claims that if G is the centroid (point of concurrence of the medians) of triangle ABC, then the areas of triangles ABG, BCG, and ACG are all equal.
2. Visualizing the scenario:
- The centroid G divides each median into a ratio of 2:1.
- Each median divides the triangle into two smaller triangles of equal area.
3. Considering the areas:
- Since G is the centroid, it divides the triangle into three smaller triangles (ABG, BCG, ACG) that share the same height from point G to line BC.
- The bases of these triangles (segments AB, BC, and AC) are also equal in proportion since G is the centroid.
4. Conclusion for Statement 2:
- Therefore, the areas of triangles ABG, BCG, and ACG are indeed equal.
- Thus, Statement 2 is also correct.
Final Conclusion
Both statements are correct. Therefore, the answer is:
Both Statement 1 and Statement 2 are correct.
1. Understanding the statement: We have triangle ABC with point D on side BC. The statement claims that if the area of triangle ABD is equal to the area of triangle ACD, then for any point O on line AD, the area of triangle ABO will equal the area of triangle ACO.
2. Visualizing the scenario:
- Let the area of triangle ABD = Area of triangle ACD = k (some constant).
- Since D divides BC into two segments such that the areas of triangles ABD and ACD are equal, line AD bisects the area of triangle ABC.
- Any point O on line AD will create two smaller triangles, ABO and ACO.
- Since O lies on AD, the heights from O to line BC for both triangles ABO and ACO will be proportional to the segments AD is divided into by point O.
- Since the areas of triangles ABO and ACO depend on the same base (line segment BC) and the heights from point A to line BC are equal, the areas of triangles ABO and ACO will also be equal.
- Therefore, Statement 1 is correct.
1. Understanding the statement: The second statement claims that if G is the centroid (point of concurrence of the medians) of triangle ABC, then the areas of triangles ABG, BCG, and ACG are all equal.
- The centroid G divides each median into a ratio of 2:1.
- Each median divides the triangle into two smaller triangles of equal area.
- Since G is the centroid, it divides the triangle into three smaller triangles (ABG, BCG, ACG) that share the same height from point G to line BC.
- The bases of these triangles (segments AB, BC, and AC) are also equal in proportion since G is the centroid.
- Therefore, the areas of triangles ABG, BCG, and ACG are indeed equal.
- Thus, Statement 2 is also correct.
Both statements are correct. Therefore, the answer is:
Both Statement 1 and Statement 2 are correct.
Similar Questions
AD is a median of triangle ABC. G is a mid point of AD. If area of triangle ABC is 16 sq. cm. Find the area of triangle GDC
View SolutionAny point D is taken on the side BC of a ΔABC and AD is produced to E such that AD = DE , prove that area of ΔBCE= area of ΔABC,
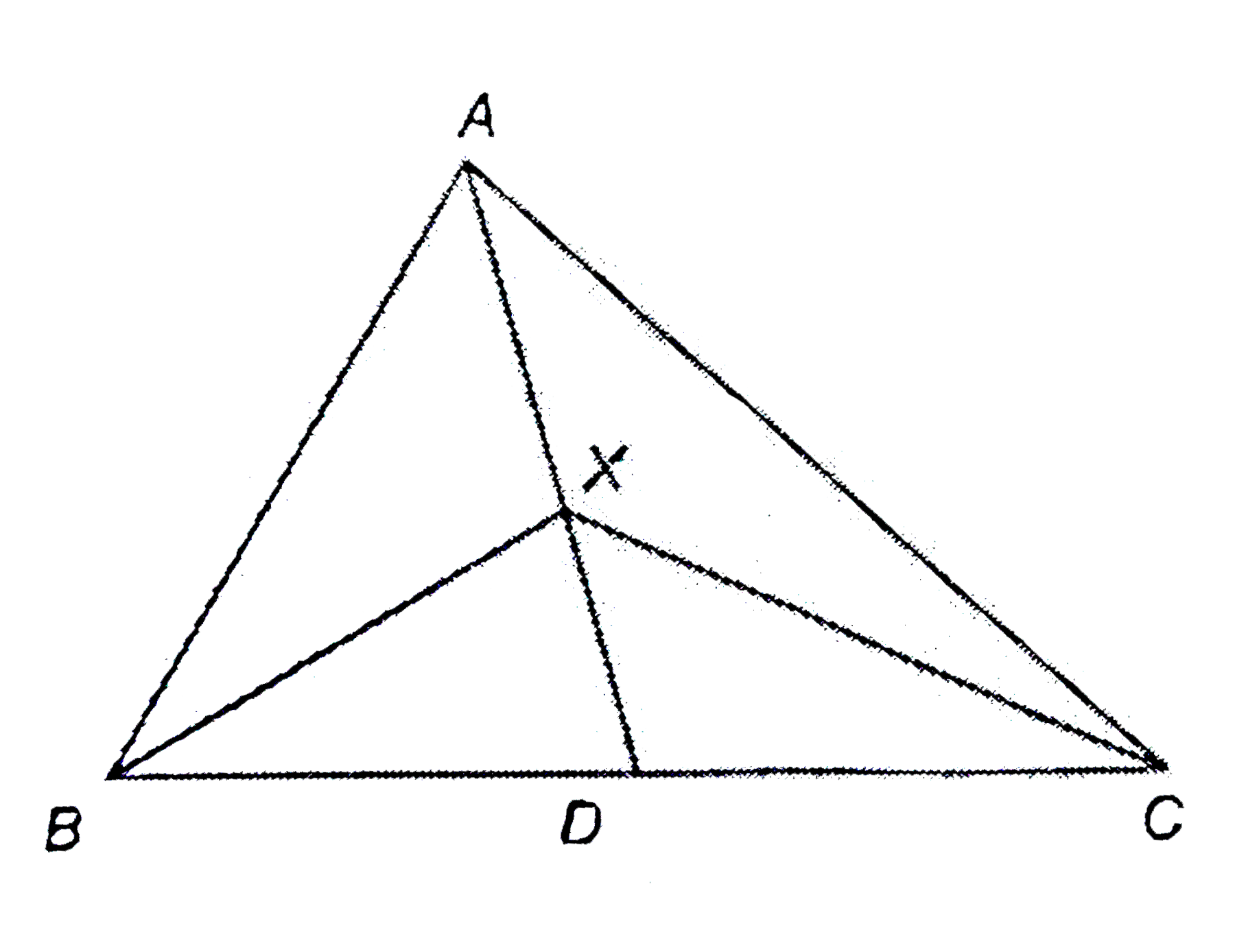
View SolutionIn the adjoining figure, AD is the median of ΔABC and X be any point on side AD. Prove that:
area (ΔABX)= area (ΔACX)
View SolutionThe medians of ΔABC intersect at point G. Prove that:
area of ΔAGB=13× area of ΔABC
View SolutionIn △ABC , the medians AD, BE and CF meet at O. What is the ratio of the area of △ABD to the area of △AOE ?
View SolutionIn △ABC, the medians AD. BE and CF meet at O. What is the ratio of the area of △ABD to the area of △AOE ?
View Solutiontriangle In ABC, the medians AD, BE and CF meet at point O. triangle ABD and triangle What will be the ratio of the areas of AOE?
View SolutionIf triangle D is a point on BC in ABC such that BD:BC= 2:5 then area ( triangle ABD) Area ( triangle What will be the ratio of ADC)?
View Solution
