In a triangle ABC, the sides AB, AC are produced and the bisectors of exterior angles of ∠ABCand∠ACB intersect at D. If ∠BAC=50∘, then ∠BDC is equal to
A)115∘
B)65∘
C)55∘
D)40∘
To solve the problem, we need to find the measure of angle BDC in triangle ABC, given that angle BAC is 50 degrees.
1. Understanding the Triangle and Angles:
- We have triangle ABC with angle BAC = 50 degrees.
- The sides AB and AC are extended, creating exterior angles at B and C.
2. Identifying the Exterior Angles:
- The exterior angle at B is given by:
Exterior angle at B=180∘−∠ABC
- The exterior angle at C is given by:
Exterior angle at C=180∘−∠ACB
3. Using the Angle Bisector Theorem:
- The angle bisector of an exterior angle divides it into two equal parts.
- Let ∠ABC=x and ∠ACB=y.
- By the triangle angle sum property, we know:
∠A+∠B+∠C=180∘
Thus:
50∘+x+y=180∘⟹x+y=130∘
4. Finding the Angles:
- The exterior angle bisector at B will create two angles of:
180∘−x2
- The exterior angle bisector at C will create two angles of:
180∘−y2
5. Finding Angle BDC:
- The angle BDC is formed by the intersection of the two exterior angle bisectors.
- According to the theorem regarding the intersection of exterior angle bisectors:
∠BDC=90∘−∠A2
- Substituting the value of angle A (which is 50 degrees):
∠BDC=90∘−50∘2=90∘−25∘=65∘
Final Answer:
∠BDC=65∘
- We have triangle ABC with angle BAC = 50 degrees.
- The sides AB and AC are extended, creating exterior angles at B and C.
- The exterior angle at B is given by:
Exterior angle at B=180∘−∠ABC
- The exterior angle at C is given by:
Exterior angle at C=180∘−∠ACB
- The angle bisector of an exterior angle divides it into two equal parts.
- Let ∠ABC=x and ∠ACB=y.
- By the triangle angle sum property, we know:
∠A+∠B+∠C=180∘
Thus:
50∘+x+y=180∘⟹x+y=130∘
- The exterior angle bisector at B will create two angles of:
180∘−x2
- The exterior angle bisector at C will create two angles of:
180∘−y2
- The angle BDC is formed by the intersection of the two exterior angle bisectors.
- According to the theorem regarding the intersection of exterior angle bisectors:
∠BDC=90∘−∠A2
- Substituting the value of angle A (which is 50 degrees):
∠BDC=90∘−50∘2=90∘−25∘=65∘
∠BDC=65∘
Similar Questions
In the adjacent figure, ABC is a triangle in which ∠B=50∘ and ∠C=70∘ . Sides AB and AC are produced. If ‘z’ is the measure of the angle between the bisectors of the exterior angles so formed, then find 'z'.
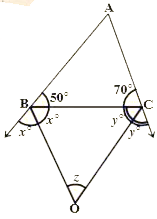
View SolutionIn the adjacent figure, ABC is a triangle in which ∠B=50∘ and ∠C=70∘ . Sides AB and AC are produced. If ‘z’ is the measure of the angle between the bisectors of the exterior angles so formed, then find 'z'.
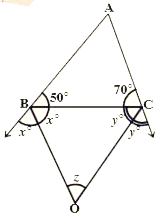
View SolutionIn the adjacent figure, ABC is a triangle in which ∠B=50∘ and ∠C=70∘ . Sides AB and AC are produced. If ‘z’ is the measure of the angle between the bisectors of the exterior angles so formed, then find 'z'.
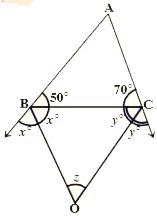
View SolutionIn the adjacent figure, ABC is a triangle in which ∠B=50∘ and ∠C=70∘ . Sides AB and AC are produced. If ‘z’ is the measure of the angle between the bisectors of the exterior angles so formed, then find 'z'.
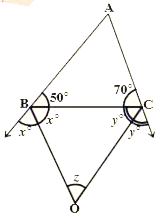
View SolutionThe bisectors of the angles B and C of an isosceles triangle with AB = AC intersect at O. Show that angle ABC An adjacent exterior angle BOC Is equal to.
View SolutionABC is a right angled triangle, in which AB = AC and angle C The bisector arm of AB intersects AB at D. Prove that AC+AD=BC is.
View SolutionABC is the hypotenuse of a right angled isosceles triangle angleBAC - The bisector of AD intersects BC at point D. Prove AC + CD = AB.
View SolutionABC is a triangle. interior angle angleB and exterior angles angleC The bisectors of C intersect at D. If angleBDC=50^(@) So angleA how much ?
View Solution
