Mass = 10kg hanging, area of cross section 100cm2, length 20cm, y=2x1011. Find total elongation.
To find the total elongation of the hanging mass, we can use the formula derived from Young's modulus:
ΔL=F⋅LY⋅A
Where:
- ΔL = elongation
- F = force applied (weight of the mass)
- L = original length of the material
- Y = Young's modulus
- A = cross-sectional area
1. Calculate the Force (Weight) Acting on the Material:
F=m⋅g
Given:
- Mass m=10kg
- Acceleration due to gravity g=10m/s2
Therefore:
F=10kg⋅10m/s2=100N
Hint: Remember that weight is the product of mass and gravitational acceleration.
2. Convert the Length from cm to m:
L=20cm=20×10−2m=0.2m
Hint: Always convert units to SI units for consistency in calculations.
3. Convert the Cross-Sectional Area from cm² to m²:
A=100cm2=100×10−4m2=0.01m2
Hint: Area conversion is crucial; remember that 1cm2=10−4m2.
4. Substitute the Values into the Young's Modulus Formula:
Given:
- Young's modulus Y=2×1011N/m2
Now substitute F, L, Y, and A into the elongation formula:
ΔL=F⋅LY⋅A=100N⋅0.2m(2×1011N/m2)⋅(0.01m2)
5. Calculate the Elongation:
ΔL=202×1011⋅0.01=202×109=202×10−9=10×10−9=10−8m
Therefore:
ΔL=10−8m=0.00001m=0.01cm
Hint: Ensure to simplify the fractions carefully and keep track of your powers of ten.
Final Result:
The total elongation of the hanging mass is 0.01cm.
- ΔL = elongation
- F = force applied (weight of the mass)
- L = original length of the material
- Y = Young's modulus
- A = cross-sectional area
F=m⋅g
Given:
- Mass m=10kg
- Acceleration due to gravity g=10m/s2
F=10kg⋅10m/s2=100N
L=20cm=20×10−2m=0.2m
A=100cm2=100×10−4m2=0.01m2
Given:
- Young's modulus Y=2×1011N/m2
ΔL=F⋅LY⋅A=100N⋅0.2m(2×1011N/m2)⋅(0.01m2)
ΔL=202×1011⋅0.01=202×109=202×10−9=10×10−9=10−8m
ΔL=10−8m=0.00001m=0.01cm
The total elongation of the hanging mass is 0.01cm.
Topper's Solved these Questions
- JEE MAIN 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2021Exercise:SECTION-A
Explore 80 Videos
- JEE MAIN 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2021Exercise:SECTION-B
Explore 40 Videos
- JEE MAINBook:JEE MAINS PREVIOUS YEARChapter:JEE MAINExercise:All Questions
Explore 473 Videos
- JEE MAIN 2022Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2022Exercise:Question
Explore 492 Videos
Similar Questions
A solenoid of length 20cm, area of cross- section 4.0cm2 and having 4000 turns is placed inside another solenoid of 2000 turns having a cross - sectional area 8.0cm ^2 and length 10 cm. Find the mutual inductance between the solenoids.
View SolutionA steel rod (Y=2.0×1011N/m2 and α=10−50.∘C−1) of length 1 m and area of cross-section 1 cm2 is heated from 0.∘C to 200∘C, without being allowed to extend or bend. What is the tension produced in the rod?
View Solution
Knowledge Check
A unifrom steel rod of length 1m and area of cross-section 20cm2 is hanging from a fixed support. Find the increases in the length of the rod.
A1.923×10−5cmB2.923×10−5cmC1.123×10−5cmD3.123×10−5cmCalculate the work done in stretching a steel wire of Young's modulus of 2×1011Nm−2, mass of 40 kg, length of 200 cm and area of cross-section is 0.06cm2~ slowly applied without the elastic limit being reached.
A2.502 jB1.103 jC0.9 jD0.128 jFor a toroid N = 500, radius = 40 cm, and area of cross section =10cm2. Find inductance
A125μHB250μHC0.00248 HDzero
A uniform heavy rod of weight 10 kg ms−2, cross-sectional area 100 cm2 and length 20 cm is hanging from a fixed support. Young modulus of the material of the rod is 2×1011Nm−2 Neglecting the lateral contraction, find the elongation of rod due to its own weight:
View SolutionA wire of length 10 cm and area of cross section 1mm2 has a resistance of 5Ω. Find the resistivity of the material of the wire.
View SolutionA coil having 800 turns, area of cross section 12cm2 and 15 cm long is connected in series with another coil having 500 turns, area of cross section 10cm2 and 10 cm long. Calculate the net inductance of the system.
View SolutionThree rods of same material, same area of cross section but different lengths 10 cm, 20 cm and 30 cm are connected at a point as shown. What is temperature of junction O?
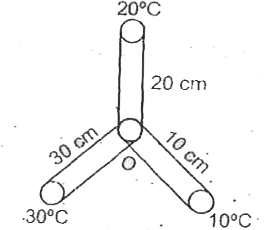
View SolutionWhat is the self - inductance of a solenoid of length 40 cm , area of cross - section 20cm2 and total number of turns 800 .
View Solution
