Moment of inertia of a square plate of side l about the axis passing through one of the corner and perpendicular to the plane of square plate is given by :
23Ml2
Ml212
Ml26
Ml2
To find the moment of inertia of a square plate of side l about an axis passing through one of its corners and perpendicular to the plane of the square plate, we can follow these steps:
1. Identify the Geometry:
We have a square plate with side length l. We need to find the moment of inertia about an axis that passes through one of its corners.
2. Use the Parallel Axis Theorem:
The parallel axis theorem states that:
I=Icm+md2
where I is the moment of inertia about the new axis, Icm is the moment of inertia about the center of mass axis, m is the mass of the plate, and d is the distance between the center of mass axis and the new axis.
3. Calculate the Moment of Inertia about the Center of Mass:
For a square plate, the moment of inertia about an axis through its center and perpendicular to the plane is given by:
Icm=16ml2
4. Determine the Distance d:
The distance d from the center of mass to the corner through which the new axis passes can be calculated. The center of mass of the square plate is located at the center, which is at (l2,l2). The distance d to the corner (0,0) can be calculated using the Pythagorean theorem:
d=√(l2)2+(l2)2=√l24+l24=√l22=l√2
5. Calculate d2:
d2=(l√2)2=l22
6. Substitute into the Parallel Axis Theorem:
Now substituting Icm and d2 into the parallel axis theorem:
I=Icm+md2=16ml2+m(l22)
7. Combine the Terms:
I=16ml2+36ml2=46ml2=23ml2
8. Final Result:
Therefore, the moment of inertia of the square plate about the axis passing through one of the corners and perpendicular to the plane of the square plate is:
I=23ml2
We have a square plate with side length l. We need to find the moment of inertia about an axis that passes through one of its corners.
The parallel axis theorem states that:
I=Icm+md2
where I is the moment of inertia about the new axis, Icm is the moment of inertia about the center of mass axis, m is the mass of the plate, and d is the distance between the center of mass axis and the new axis.
For a square plate, the moment of inertia about an axis through its center and perpendicular to the plane is given by:
Icm=16ml2
The distance d from the center of mass to the corner through which the new axis passes can be calculated. The center of mass of the square plate is located at the center, which is at (l2,l2). The distance d to the corner (0,0) can be calculated using the Pythagorean theorem:
d=√(l2)2+(l2)2=√l24+l24=√l22=l√2
d2=(l√2)2=l22
Now substituting Icm and d2 into the parallel axis theorem:
I=Icm+md2=16ml2+m(l22)
I=16ml2+36ml2=46ml2=23ml2
Therefore, the moment of inertia of the square plate about the axis passing through one of the corners and perpendicular to the plane of the square plate is:
I=23ml2
Topper's Solved these Questions
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B)
40 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section A )
20 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics Section B
20 Videos
- JEE MAINS 2020BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2020EXERCISE - PHYSICS
246 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -B)
10 Videos
Similar Questions
The moment of inertia of a square plate of mass 4kg and side 1m about an axis passing through its centre and perpendicular to its plane is
View SolutionThe moment of inertia of a thin square plate ABCD of uniform thickness about an axis passing through its center and perpendicular to its plane will

View Solution
Knowledge Check
The moment of inertia of a thin square plate ABCD of uniform thickness about an axis passing through the centre O and perpendicular to the plane of the plate is
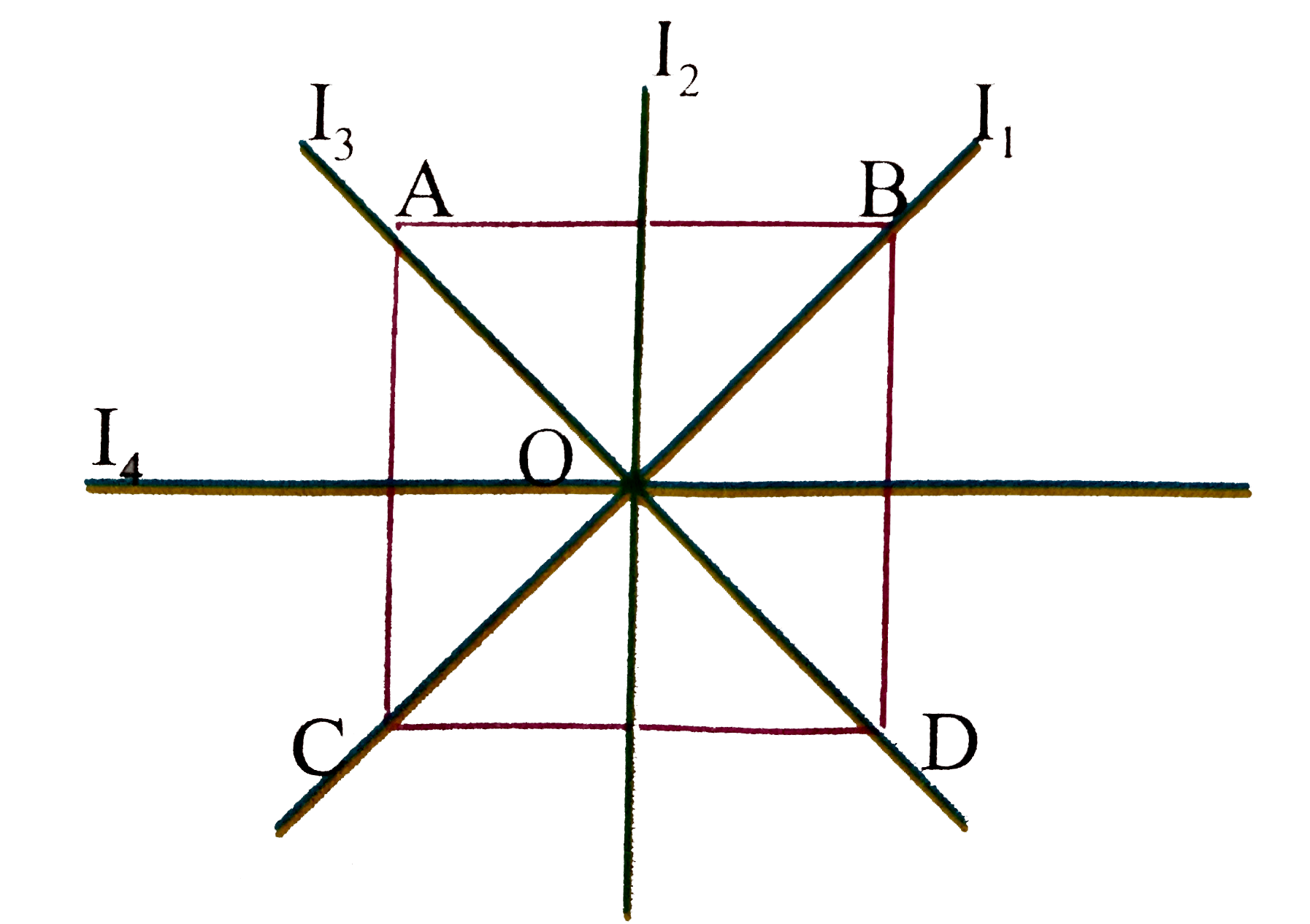
(a)I1+I2, (b)I2+I4
2I1+I3, (d) I1+2I3Aa,b are trueBb,c are trueCc,d are trueDb,d are trueThe moment of inertia of a thin square plate ABCD of uniform thickness about an axis passing through the centre O and perpendicular to plate is
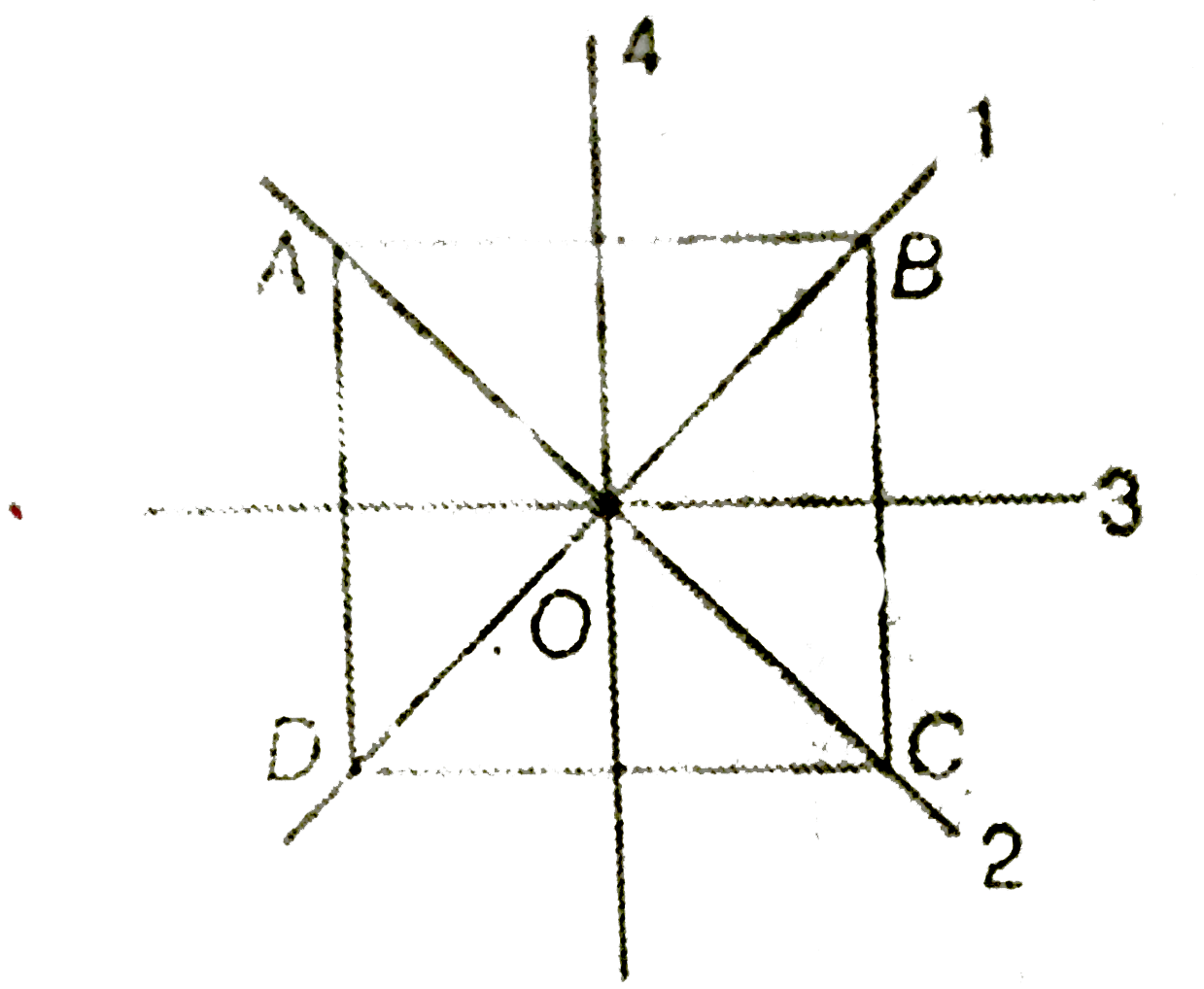 Al1+l2Bl2+l3Cl1+l3Dl3+l4
Al1+l2Bl2+l3Cl1+l3Dl3+l4The moment of inertia of a thin square plate ABCD, fig, of uniform thickness about an axis passing through the centre O and perpendicular to the plane of the plate is
where l1,l2,l3andl4 are respectively the moments of intertial about axis 1,2,3 and 4 which are in the plane of the plate.
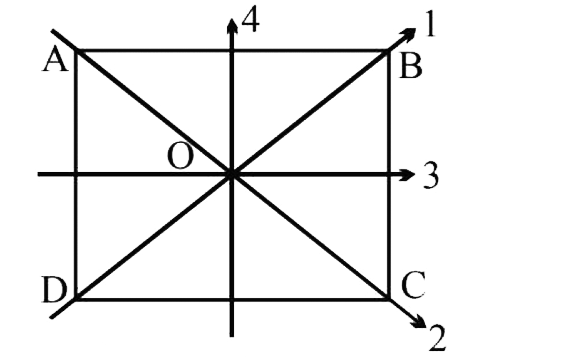 Al1+l2Bl3+l4Cl1+l3Dl1+l2+l3+l4
Al1+l2Bl3+l4Cl1+l3Dl1+l2+l3+l4
Find moment of inertia of a uniform rectangular plate about axis zz' passing through center and perpendicular to the plane of plate, as shown in Fig.

View SolutionIn the above problem, calculate the moment of inertia about an axis passing through point Q and perpendicular to the plane of square.
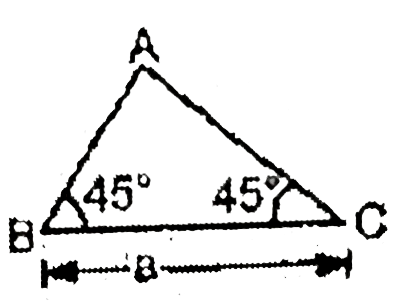
View SolutionWhat is the moment of inertia of a triangular plate ABC of mass M and side BC='a' about a axis passing through A and perpedicular to the plane of the plate?
View SolutionA square plate of edge a/2 is cut out from a uniform square plate of edge 'a' shown in figure. The mass of the remaining portion is M. The moment of inertia of the shaded portion about an axis passing through 'O'( centre of the square of side a) and perpendicular to plane of the plate is :

View SolutionFour masses 1, 2, 3 and 4 kg each are placed on four corners A, B, C and D of a square of side √2 m. The moment of inertia of this system about an axis passing through the point of inter-section of diagonals and perpendicular to the plane of the square will be:
View Solution

