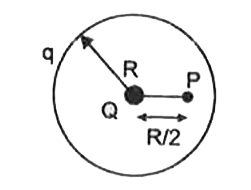
A thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point p a distance R/2 from the centre of the shell is :
(q+Q)4πε02R
2Q4πε0R
2Q4πε0R=2q4πε0R
2Q4πε0R+q4πε0R
The correct Answer is:D
Electric potential at P
V=k.QR/2+k.qR
=2Q4πε0R+q4πε0R
Topper's Solved these Questions
- ELECTROSTATICSBOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - LEVEL -II
57 Videos
- ELECTROSTATICSBOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - LEVEL-III
21 Videos
- ELECTRONS & PHOTONSBOOK - MODERN PUBLICATIONCHAPTER - ELECTRONS & PHOTONSEXERCISE - RECENT COMPETITIVE QUESTIONS
20 Videos
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - Recent Competitive Questions
7 Videos
Similar Questions
A charge + Q is uniformly distributed over a thin ring of the radius R. The velocity of an electron at the moment when it passes through the centre O of the ring, if an electron was initially at rest at a point A which is very far always from the centre and on the axis of the ring is :
View SolutionTwo positive charges of magnitude 'q' are placed at the ends of a side (side 1 ) of a square of side 2a . Two negative charges of the same magnitude are kept at the other corners . Starting from rest , if a charge Q moves from the middle of side 1 to the centre of square , its kinetic energy at the centre of square is :
View SolutionAccording to Einstein's photoelectric equation the graph of K.E. of the photoelectron emitted from the metal versus the frequency of the incident radiation gives a straight line graph whose slope
View SolutionAn astronaut on a strange planet finds that acceleration due to gravity is twice as that on the surface of earth. Which of the following could explain thin ?
View SolutionA thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P a distance R/2 from the centre of the shell is
View SolutionThe electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre
View SolutionA point charge +Q is placed at the centre of an isolated conducting shell of radius R. Find the electrostatic potential energy stored outside the spherical shell if the shell also contains charge +Q distributed uniformly over it.
View SolutionA point charge Q is placed inside a conducting spherical shell of inner radius 3R and outer radius 5R at a distance R from the centre of the shell. The electric potential at the centre of the shell will be
View SolutionA point charge Q is placed inside a conducting spherical shell of inner radius 3R and outer radius 5R at a distance R from the centre of the shell. The electric potential at the centre of the shell will be
View SolutionA thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P at a distance R/2 from the centre of the shell is
View SolutionA point charge Q is placed inside a conducting spherical shell of inner radius 3R and outer radius 5R at a distance R from the centre of the shell. The electric potential at the centre of the shell will be.
View SolutionThe electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre
View SolutionA thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P a distance R/2 from the centre of the shell is
View SolutionA thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P a distance R/2 from the centre of the shell is
View SolutionA thin metallic spherical shell of radius R carries a charge Q on its surface. A point charge Q/2 is placed at its centre C and another charge +2Q outside the shell at a distance r from the centre as shown in figure. Find the force on the charge at the centre of shell and at point A.
View Solution

