If P(x)=(x3−8)(x+1)andQ(x)=(x3+1)(x−2), then find the LCM of P(x)andQ(x).
(x−2)(x+1)
(x2+2x+4)(x2+4x+1)
(x+1)2(x−2)2(x2+2x+4)(x2+4x+1)
(x+1)(x−2)(x2+2x+4)(x2−x+1)
The correct Answer is:D
To find the LCM of the polynomials P(x) and Q(x), we will first factor both polynomials using the relevant algebraic identities.
Step 1: Factor P(x)
Given:
P(x)=(x3−8)(x+1)
We can factor x3−8 using the difference of cubes formula:
a3−b3=(a−b)(a2+ab+b2)
Here, a=x and b=2:
x3−8=(x−2)(x2+2x+4)
Thus, we can rewrite P(x):
P(x)=(x−2)(x2+2x+4)(x+1)
Step 2: Factor Q(x)
Given:
Q(x)=(x3+1)(x−2)
We can factor x3+1 using the sum of cubes formula:
a3+b3=(a+b)(a2−ab+b2)
Here, a=x and b=1:
x3+1=(x+1)(x2−x+1)
Thus, we can rewrite Q(x):
Q(x)=(x+1)(x2−x+1)(x−2)
Step 3: Find the LCM of P(x) and Q(x)
To find the LCM, we take the highest power of each factor from both polynomials:
- From P(x): (x−2),(x2+2x+4),(x+1)
- From Q(x): (x+1),(x2−x+1),(x−2)
The LCM will be:
LCM=(x−2)(x+1)(x2+2x+4)(x2−x+1)
Final LCM Expression
Thus, the LCM of P(x) and Q(x) is:
LCM(P(x),Q(x))=(x−2)(x+1)(x2+2x+4)(x2−x+1)
P(x)=(x3−8)(x+1)
We can factor x3−8 using the difference of cubes formula:
a3−b3=(a−b)(a2+ab+b2)
Here, a=x and b=2:
x3−8=(x−2)(x2+2x+4)
Thus, we can rewrite P(x):
P(x)=(x−2)(x2+2x+4)(x+1)
Q(x)=(x3+1)(x−2)
We can factor x3+1 using the sum of cubes formula:
a3+b3=(a+b)(a2−ab+b2)
Here, a=x and b=1:
x3+1=(x+1)(x2−x+1)
Thus, we can rewrite Q(x):
Q(x)=(x+1)(x2−x+1)(x−2)
- From P(x): (x−2),(x2+2x+4),(x+1)
- From Q(x): (x+1),(x2−x+1),(x−2)
LCM=(x−2)(x+1)(x2+2x+4)(x2−x+1)
Thus, the LCM of P(x) and Q(x) is:
LCM(P(x),Q(x))=(x−2)(x+1)(x2+2x+4)(x2−x+1)
Topper's Solved these Questions
Similar Questions
Let f(x) =a0xn+a1xn−1+...+an(a0≠0) be a polynomial of degree n . If x+1 is one of its factors, then______.
View SolutionStudy the following information carefully and answer the questions given below it.
Sheena and Bhanu threw a dice 20-20 times and got following results Sheena
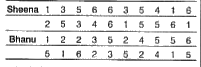
Which number occured least number of times?
View SolutionP=x^(3)-(1)/(x^(3)),Q=x-(1)/(x)x in(1,oo) then minimum value of (P)/(sqrt(3)Q^(2))
View Solutionनिम्नलिखित में से प्रत्येक में p(x) को q(x) से गुणा कीजिए और इस गुणनफल की घात ज्ञात कीजिए :
(i) p(x)=x2−2x+1 और q(x)=x3−3x2+2x−1
(ii) p(x)=x2+2x+3 और q(x)=x−1.
View Solutionनिम्नलिखित में ज्ञात कीजिए और बहुपद की घात बताइए :
(i) p(x)=x3−1,q(x)=x−1
(ii) p(x)=x4+2x3+5x2+7x,q(x)=x.
View Solutionयदि p(x)=x2−5x+4 तथा q(x)=x3+1तो के मान ज्ञात करे।
p(1)q(1)
View Solutionयदि p(x)=x3−3x2+3x−5 एवं q(x)=x−1 तो p(x) को q(x) से भाग दे तथा भागफल एवं शेषफल ज्ञात करे। क्या p(x) का एक गुणनखंड q(x) है?
View Solutionp(x).q(x) ज्ञात कीजिये एवं प्रत्येक में उसका घात लिखिए, जब
p(x)=1+x+x2+x3+x4 एवं q(x)=1+x−x2
View Solutionयदि p(x)=x3−2x2+x−1 और q(x)=x−2 तो p(x) को q(x) से भाग देने पर शेषफल ज्ञात कीजिये।
View Solutionयदि p(x)=x2+x+1,तो बहुपद q(x) निकालें ताकि p(x)⋅q(x)=x3−1.
View SolutionLCM of the polynomials P and Q, where
P=(x−2)(x+1)2(x+3)2
Q=(x+1)2(x+3)(x+4) is given by :
View Solutionयदि P=x3+3x−1 तथा Q=x−12x हो ,तो PQ ज्ञात कीजिए।
View SolutionFind the LCM and HCF of the polynomials P(x)=(x+1)2(x+2)
Q(x)=(x+1)(x−2)
View SolutionIf HCF and LCM of two polynomial P(x) & Q(x) is (a+1)anda3+a2−a−1 respectively if P(x)=(a2−1), find Q(x)= ?
View Solutionदो बहुपदो P(x) एवं Q(x) का म.स. (x+1)(x2+1) है और उनका ल.स. x4−1 है। यदि P(x)=x3+x2+x+1, तो Q(x) ज्ञात कीजिए।
View SolutionP=x3−1x3,Q=x−1x x∈(1,∞) then minimum value of P√3Q2
View Solution
