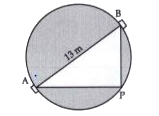
In the Dwarika residency colony, there is a circular park of diameter 13 metres. A pole has to erected at the point P on the boundary of circular park in such a way that the difference of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres.
In an equation does not have real roots, then it is said to be having ................... roots.
real
equal
imaginary
none of these
Step by step video solution for In the Dwarika residency colony, there is a circular park of diameter 13 metres. A pole has to erected at the point P on the boundary of circular park in such a way that the difference of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. In an equation does not have real roots, then it is said to be having ................... roots. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRATIC EQUATIONSBOOK - OSWAL PUBLICATIONCHAPTER - QUADRATIC EQUATIONSEXERCISE - SELF ASSESSMENT -2 (Multiple Choice Questions:)
3 Videos
- QUADRATIC EQUATIONSBOOK - OSWAL PUBLICATIONCHAPTER - QUADRATIC EQUATIONSEXERCISE - SELF ASSESSMENT -2 (Fill in the Blanks:)
3 Videos
- QUADRATIC EQUATIONSBOOK - OSWAL PUBLICATIONCHAPTER - QUADRATIC EQUATIONSEXERCISE - SELF ASSESSMENT -1 (Long Answer Type Questions-III)
2 Videos
- PROBABILITYBOOK - OSWAL PUBLICATIONCHAPTER - PROBABILITYEXERCISE - Self Assessment
66 Videos
- REAL NUMBERSBOOK - OSWAL PUBLICATIONCHAPTER - REAL NUMBERSEXERCISE - Self-Assessment
11 Videos
Similar Questions
The value of p for which the quadratic equation 4x2+px+3=0 has equal roots are.
View SolutionNature of roots of quadratic equation 4x2+3x−14=0 is…..
View SolutionGiven, solve for x:(2xx−5)2+5(2xx−5)−24=0,x≠5
View SolutionA bag contains 5 red balls and some blue balls. If the probability of drawing a blue ball from the bag is double that of a red ball, find the number of blue balls in the bag.
View SolutionFind the H.C.F. of x2+3x–10andx3−8x.
View SolutionA pole has to be erected at a point on the boundary of a circular park of diameter 13 metres in such a way that the differences of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. Is it possible to do so? If yes, at what distances from the two gates should the pole be erected?
View SolutionA pole has to be erected at a point on the boundary of a circular park of diameter 13 metres in such a way that the difference of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. Is it the possible to do so? If yes, at what distances from the two gates should the pole be erected?
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionMatch the following Column A to Column B

View SolutionA pole has to be erected at a point on the boundary of a circular ground of diameter 20m in such a way that the difference of its distance form two diameterically opposite fixed gates P and Q on the boundary is 4 m. Is it possible to do so? If answer is yes at what distance from the two gates should the pole be erected?
View SolutionA pole has to be erected at a point on the boundary of a circular park of diameter 13 metres in such a way that the differences opposite fixed gates A and B on the boundary is 7 metres. Is it possible to do so ? If yes, at what distances from the two gates should the pole be erected ?
View Solution13 cm. It was intended to erect a pillar on the boundary of a circular park of diameter. The distance from the two gates A and B, which are arranged opposite the boundary of the park, i.e. at the end points of a diameter, to this pillar is 7 m. Can the pillar be set up as it is? If so, how far is this pillar from the two gates?
View SolutionOne root of the equation x2+ax+3=0 is 1.Find the value of a.
View SolutionA pole has to be erected at a point on the boundary of a circular park of diameter 13 metres in such a way that the differences of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. Is it possible to do so? If yes, at what distances from the two gates should the pole be erected?
View SolutionA pole has to be erected at a point on the boundary of a circular park of diameter 13 metres in such a way that the differences of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. Is it possible to do so? If yes, at what distances from the two gates should the pole be erected?
View SolutionA pole has to be erected at a point on the boundary of a circular park of diameter 13 metres in such a way that the differences of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. Is it possible to do so? If yes, at what distances from the two gates should the pole be erected?
View Solution
