In the following question, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): If the median and mode of a frequency distribution are 150 and 154 respectively. Then its mean is 148.
Reason (R): Mean, median and mode of a frequency distribution are related as 3Mean=3Median - Mode.
Both A and R are true and R is the correct explanation for A.
Both A and R are true and R is not correct explanation for A.
A is true but R is false.
A is false but R is true.
The correct Answer is:A
To solve the problem, we need to analyze the given assertion and reason statements regarding the relationship between mean, median, and mode in a frequency distribution.
1. Understand the Assertion (A):
- The assertion states that if the median is 150 and the mode is 154, then the mean is 148.
2. Understand the Reason (R):
- The reason states that the relationship between mean, median, and mode is given by the formula:
3×Mean=3×Median−Mode
3. Check the Given Formula:
- The correct relationship is:
Mode=3×Median−2×Mean
- However, the reason provided in the question is incorrect.
4. Use the Correct Formula:
- Rearranging the correct formula gives us:
2×Mean=3×Median−Mode
- This can be rewritten as:
Mean=3×Median−Mode2
5. Substitute the Values:
- Substitute the given values of median and mode into the formula:
- Median = 150
- Mode = 154
- Plugging in these values:
Mean=3×150−1542
6. Calculate the Mean:
- Calculate 3×150:
3×150=450
- Now substitute this back into the equation:
Mean=450−1542
- Calculate 450−154:
450−154=296
- Now divide by 2:
Mean=2962=148
7. Conclusion:
- The calculated mean is indeed 148, which confirms the assertion is correct.
- However, the reason provided is incorrect because the formula stated is not the standard relationship between mean, median, and mode.
Final Answer:
- The assertion (A) is true, and the reason (R) is false. Therefore, the correct choice is that the assertion is correct, but the reason is incorrect.
- The assertion states that if the median is 150 and the mode is 154, then the mean is 148.
- The reason states that the relationship between mean, median, and mode is given by the formula:
3×Mean=3×Median−Mode
- The correct relationship is:
Mode=3×Median−2×Mean
- However, the reason provided in the question is incorrect.
- Rearranging the correct formula gives us:
2×Mean=3×Median−Mode
- This can be rewritten as:
Mean=3×Median−Mode2
- Substitute the given values of median and mode into the formula:
- Median = 150
- Mode = 154
- Plugging in these values:
Mean=3×150−1542
- Calculate 3×150:
3×150=450
- Now substitute this back into the equation:
Mean=450−1542
- Calculate 450−154:
450−154=296
- Now divide by 2:
Mean=2962=148
- The calculated mean is indeed 148, which confirms the assertion is correct.
- However, the reason provided is incorrect because the formula stated is not the standard relationship between mean, median, and mode.
- The assertion (A) is true, and the reason (R) is false. Therefore, the correct choice is that the assertion is correct, but the reason is incorrect.
টপার এই প্রশ্নগুলো সমাধান করেছে
- STATISTICSBook:OSWAL PUBLICATIONChapter:STATISTICSExercise:CASE BASED MCQs
Explore 15 Videos
- STATISTICSBook:OSWAL PUBLICATIONChapter:STATISTICSExercise:Example
Explore 3 Videos
- STATISTICSBook:OSWAL PUBLICATIONChapter:STATISTICSExercise:Assertion and Reasoning Based Questions
Explore 2 Videos
- SOME APPLICATIONS OF TRIGONOMETRY (HEIGHTS AND DISTANCES) Book:OSWAL PUBLICATIONChapter:SOME APPLICATIONS OF TRIGONOMETRY (HEIGHTS AND DISTANCES) Exercise:CASE-BASED MCQs
Explore 15 Videos
- SURFACE AREAS AND VOLUMES Book:OSWAL PUBLICATIONChapter:SURFACE AREAS AND VOLUMES Exercise:BOARD CORNER (LONG ANSWER TYPE QUESTIONS)
Explore 9 Videos
সম্পর্কিত প্রশ্ন
If the mean and mode of a frequency distribution be 53.4 and 55.2 respectively, find the median
View SolutionIn the following question, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): Mean of given data is 13.81

Reason (R): Mean= ∑FX∑F
View Solution
জ্ঞান পরীক্ষা করুন
The median and mode of a frequency distribution are 26 and 29 respectively. Then , the mean is
A27.5B24.5C28.4D25.8The mean and mode of a frequency distribution are 28 and 16 respectively .The median is
A22B23.5C24D24.5Mean and median of a simple distribution are 38 and 39 respectively. Then, mode will be
A36B37C41D40
Find the mean and median of the following distribution :
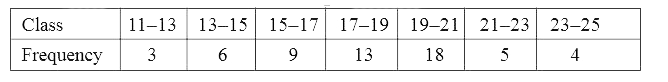
View SolutionFind the median marks for the following frequency distribution :

View SolutionRelation between mean, median and mode -
View SolutionIf in a frequency distribution, the mean and median are 21 and 22 respectively, then its mode is approximately
View SolutionIf the mean and median of a set of numbers are 8.2 and 8.4, respectively, then mode is
View Solution