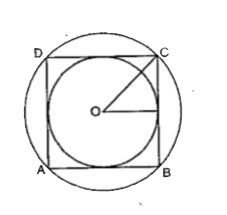
What is the area of the region bounded internally by a square of side of length ‘a’ and externally by a circle passing through the four comers of the square ?
(π−1)a2 square units
(π−1)a22 square units
(π−2)a2 square units
(π−2)a22 square units
To find the area of the region bounded internally by a square of side length a and externally by a circle passing through the four corners of the square, we can follow these steps:
Step 1: Calculate the area of the square.
The area Asquare of a square is given by the formula:
Asquare=a2
Step 2: Determine the radius of the circle.
The circle that passes through the four corners of the square is known as the circumcircle of the square. The radius R of the circumcircle can be calculated using the formula:
R=a√22
This is because the diagonal of the square is the diameter of the circle. The diagonal d of the square can be calculated as:
d=a√2
Thus, the radius R is:
R=d2=a√22
Step 3: Calculate the area of the circle.
The area Acircle of the circle is given by the formula:
Acircle=πR2
Substituting the value of R:
Acircle=π(a√22)2=π(2a24)=πa22
Step 4: Find the area of the region bounded by the square and the circle.
The area of the region bounded internally by the square and externally by the circle is given by:
Aregion=Acircle−Asquare
Substituting the areas we calculated:
Aregion=πa22−a2
Factoring out a2:
Aregion=a2(π2−1)
Final Result
Thus, the area of the region bounded internally by the square and externally by the circle is:
a2(π2−1)
The area Asquare of a square is given by the formula:
Asquare=a2
The circle that passes through the four corners of the square is known as the circumcircle of the square. The radius R of the circumcircle can be calculated using the formula:
R=a√22
This is because the diagonal of the square is the diameter of the circle. The diagonal d of the square can be calculated as:
d=a√2
Thus, the radius R is:
R=d2=a√22
The area Acircle of the circle is given by the formula:
Acircle=πR2
Substituting the value of R:
Acircle=π(a√22)2=π(2a24)=πa22
The area of the region bounded internally by the square and externally by the circle is given by:
Aregion=Acircle−Asquare
Substituting the areas we calculated:
Aregion=πa22−a2
Factoring out a2:
Aregion=a2(π2−1)
Thus, the area of the region bounded internally by the square and externally by the circle is:
a2(π2−1)
Similar Questions
If a circle is inscribed in a square of side 10, so that the circle touches the four sides of the square internally then radius of the circle is
View SolutionThe length of a side of a square is 4 cm.A circle is drawn through the four vertices of the square.Find the area of the portions between the circle and the square.
View SolutionIf a circle is inscribed in a square of side 10, so that the circle touches the four sides of the square internally then radius of the circle is
View Solutionএকটি বর্গক্ষেত্রের ক্ষেত্রফল যত বর্গসেমি এর পরিসীমা তত সেমি। বর্গক্ষেত্রটির বাহুর দৈর্ঘ্য কত?
View SolutionIf the area of region bounded by the inscribed and circumscribed circles of a square is 9π, then the area of the square will be :
View SolutionA square ABCD is inscribed in a circle of unit radius. Semicircles are described on each side as a diameter. The area of the region bounded by the four semicircles and the circle is
View SolutionThe area of the region bounded externally by a square of side 2a cm and internally by the circle touching the four sides of the square is
View SolutionFour equal circles are drawn on the four sides of a square in such a way that each of the circles touches two other circles. What will be the area outside the perimeter of the circles towards the middle of the square? If the measure of each side of the square is 28 cm
View Solution
