Equal loads are suspended using identical wires of steel and copper. Which wire is elongated more ?
To determine which wire, steel or copper, will elongate more when equal loads are suspended from them, we can use the concept of Young's modulus of elasticity. Here’s a step-by-step solution:
Step 1: Understand Young's Modulus
Young's modulus (E) is defined as the ratio of stress (force per unit area) to strain (relative change in length). Mathematically, it is given by:
E=F/AΔL/L
Where:
- E = Young's modulus
- F = Force applied (equal load in this case)
- A = Cross-sectional area of the wire
- ΔL = Change in length (elongation)
- L = Original length of the wire
Step 2: Compare Young's Modulus of Steel and Copper
The Young's modulus for steel is significantly higher than that for copper. This means that steel is stiffer than copper. For typical values:
- Young's modulus of steel Esteel≈200GPa
- Young's modulus of copper Ecopper≈110GPa
Step 3: Relate Elongation to Young's Modulus
From the formula for Young's modulus, we can rearrange it to find the elongation:
ΔL=FLAE
This shows that elongation (ΔL) is inversely proportional to Young's modulus (E).
Step 4: Analyze the Elongation for Both Wires
Since both wires are subjected to the same force (equal loads) and have the same dimensions (identical wires), we can compare their elongations:
- For steel:
ΔLsteel=FLAEsteel
- For copper:
ΔLcopper=FLAEcopper
Step 5: Conclusion
Since Esteel>Ecopper, it follows that:
ΔLsteel<ΔLcopper
Thus, the copper wire will elongate more than the steel wire when equal loads are suspended from them.
Final Answer
The copper wire is elongated more than the steel wire.
---
Young's modulus (E) is defined as the ratio of stress (force per unit area) to strain (relative change in length). Mathematically, it is given by:
E=F/AΔL/L
Where:
- E = Young's modulus
- F = Force applied (equal load in this case)
- A = Cross-sectional area of the wire
- ΔL = Change in length (elongation)
- L = Original length of the wire
The Young's modulus for steel is significantly higher than that for copper. This means that steel is stiffer than copper. For typical values:
- Young's modulus of steel Esteel≈200GPa
- Young's modulus of copper Ecopper≈110GPa
From the formula for Young's modulus, we can rearrange it to find the elongation:
ΔL=FLAE
This shows that elongation (ΔL) is inversely proportional to Young's modulus (E).
Since both wires are subjected to the same force (equal loads) and have the same dimensions (identical wires), we can compare their elongations:
- For steel:
ΔLsteel=FLAEsteel
- For copper:
ΔLcopper=FLAEcopper
Since Esteel>Ecopper, it follows that:
ΔLsteel<ΔLcopper
Thus, the copper wire will elongate more than the steel wire when equal loads are suspended from them.
The copper wire is elongated more than the steel wire.
Topper's Solved these Questions
- ELASTICITYBOOK - CENGAGE PHYSICSCHAPTER - ELASTICITYEXERCISE - MANDATORY EXERCISE (Exercise Set II) Multiple - Choice Questions with One correct Answer
21 Videos
- ELASTICITYBOOK - CENGAGE PHYSICSCHAPTER - ELASTICITYEXERCISE - CHALLENGING EXERCISE
8 Videos
- ELASTICITYBOOK - CENGAGE PHYSICSCHAPTER - ELASTICITYEXERCISE - MANDATORY EXERCISE (Exercise Set I)
6 Videos
- DESCRIPTION OF MOTIONBOOK - CENGAGE PHYSICSCHAPTER - DESCRIPTION OF MOTIONEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISE
10 Videos
- FRICTIONBOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES (Read the given statements and select the correct option.)
1 Video
Similar Questions
The length of an iron wire is L and area of cross - section is A. The increase of length l is observed on applying the force F on its two ends. Which of the following statement is correct ?
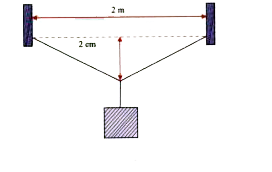
View SolutionA wire of length 2 m is fixed, as shown. When a load is suspended from the center, it sags by 2 cm. Find the strain.
View SolutionWhy are the bridges declared unsafe after long use ?
View SolutionA point moves with uniform acceleration and v1,v2 and v3 denote the average velocities in the three successive intervals of time t1,t2,andt3. Which of the following relations is correct
View SolutionAssertion: Friction is a self-adjusting force.
Reason: Friction does not depend upon mass of the body.
View SolutionIn the above question the ratio of the elongation produced in the copper wire and steel wire are
View SolutionA stone is suspended in a tub of water with copper wire. Another stone of equal mass is suspended in kerosene with equal length of copper wire then
View SolutionA copper wire and a steel wire of the same length and same cross-section are joined end to end to form a composite wire. The composite wire is hung form a rigid support and a load is suspended form the other end. If the increses in length of the composite wire is 2.4mm. then the increases in lenghts of steel and copper wires are
View SolutionTwo wire of same radius and lengh the are subjected to the same load. One wire is of steel and the other is of copper. If the Young's modulus of steel is twice that of copper, the ratio the energy stored per unit volume in steel to that of copper wire is
View SolutionIn the question number 55, the ratio of elongation of steel to the copper wires is
View SolutionA copper wire of length 2.2 m and a steel wire of length 1.6 m, both of diameter 3.0 mm, are connected end to end. When stretched by a load , the net elongation is found to be 0.70 mm. Obtain the load applied.
View SolutionA copper wire of length 2.2 m and a steel wire of length 1.6 m, both of diameter 3.0 mm, are connected end to end. When stretched by a load , the net elongation is found to be 0.70 mm. Obtain the load applied.
View SolutionA copper wire of length 2.2 m and a steel wire of length 1.6 m, both of diameter 3.0 mm, are connected end to end. When stretched by a load , the net elongation is found to be 0.70 mm. Obtain the load applied.
View SolutionA copper wire of length 2.2 m and a steel wire of length 1.6 m, both of diameter 3.0 mm, are connected end to end. When stretched by a load , the net elongation is found to be 0.70 mm. Obtain the load applied.
View SolutionTwo wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in fig. The unloaded length of steel wire is 1.5m and that of brass wire is 1.0m. Compute the elongations of the steel and the brass wires.

View SolutionA load (M) suspended from a wire produces an elongation (e ) in the wire then find the rise in temperature required to produce same elongation in the same wire.
View Solution

