ABC is a right triangle, right angled at C and AB=√2BC. Then, find ∠ABC.
The correct Answer is:45∘
To solve the problem, we will follow these steps:
Step 1: Understand the Triangle
We have a right triangle ABC, where angle C is the right angle. We know that AB=√2⋅BC.
Step 2: Assign Variables
Let:
- BC=x (the length of side BC)
- Then, AB=√2⋅x (the length of side AB)
Step 3: Use the Pythagorean Theorem
In a right triangle, the Pythagorean theorem states that:
AB2=AC2+BC2
Substituting the known lengths:
(√2⋅x)2=AC2+x2
This simplifies to:
2x2=AC2+x2
Step 4: Rearranging the Equation
Now, we can rearrange the equation to find AC2:
AC2=2x2−x2
AC2=x2
Taking the square root of both sides gives:
AC=x
Step 5: Find the Angles Using Trigonometric Ratios
Now we need to find angle ABC, which we will denote as θ.
Using the cosine ratio:
cos(θ)=BCAB
Substituting the values we have:
cos(θ)=x√2⋅x
This simplifies to:
cos(θ)=1√2
Step 6: Determine the Angle
We know that:
cos(45∘)=1√2
Thus:
θ=45∘
Final Answer
The angle ABC is 45∘.
---
We have a right triangle ABC, where angle C is the right angle. We know that AB=√2⋅BC.
Let:
- BC=x (the length of side BC)
- Then, AB=√2⋅x (the length of side AB)
In a right triangle, the Pythagorean theorem states that:
AB2=AC2+BC2
Substituting the known lengths:
(√2⋅x)2=AC2+x2
This simplifies to:
2x2=AC2+x2
Now, we can rearrange the equation to find AC2:
AC2=2x2−x2
AC2=x2
Taking the square root of both sides gives:
AC=x
Now we need to find angle ABC, which we will denote as θ.
cos(θ)=BCAB
Substituting the values we have:
cos(θ)=x√2⋅x
This simplifies to:
cos(θ)=1√2
We know that:
cos(45∘)=1√2
Thus:
θ=45∘
The angle ABC is 45∘.
Topper's Solved these Questions
- SAMPLE PAPER 8Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 8Exercise:PART-A (SECTION-II)
Explore 20 Videos
- SAMPLE PAPER 8Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 8Exercise:PART-B (SECTION-III)
Explore 9 Videos
- SAMPLE PAPER 8Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 8Exercise:SECTION-C
Explore 10 Videos
- SAMPLE PAPER 7Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 7Exercise:PART - B (SECTION - V)
Explore 8 Videos
- SAMPLE PAPER 9Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 9Exercise:SECTION C
Explore 10 Videos
Similar Questions
Jawaharlal Nehru Stadium in New Delhi is conducting the annual sports competition soon. The curator of the stadium is tasked with preparing the grounds for various sports as per the technical requirements of sports invigilator.
The engineer assigned to assist the curator is tasked with figuring out the dimensions for carving out some areas allotted for a 'hockey court' and a 'javelin range', as shown in the figure below.

The shapes of the 'hockey court' and the 'javelin range' are square and triangle respectively. Both of the courts have a common edge that touches the centre of stadium. The construction of the javelin range is such that the angle to centre is 90∘. The radius of the stadium is 200 metres.
The area (in sq m) allotted to 'javelin" range' is
View SolutionExpress 0.3528 in the form p2m5n and write the values of p, m and n.
View SolutionWhat is the shape formed by x2−8 ?
View SolutionFrom the top of a building AB, 60 metres hight, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30∘ and 60∘, respectively. Find
(i) the horizontal distance between AB and CD.
(ii) the height of the lamp post.
View SolutionCase Study-1:
Due to covid-19 lockdown, Ramesh decides to redo his house garden with some plantation work with his son. They have an equilateral triangle shaped garden and he has planted the garden with 6 different types of flowers (each of radius 1 m within a circular area). This left the remaining part of garden (that is outside the circular plants area) with lush green grass.
Now, comes the part of adding boundaries to corner the garden off nicely and he needs to know some calculations for it.
A boundary wall of height 25 cm is to be made around the garden leaving a space of 1 m wide for a gate on one side. The total length of boundary wall is
View SolutionABC is Right triangle, right angled at B such that BC = 6 and AB = 8 cm. Find the radius of its incircle.
View SolutionDraw triangle ABC with ∠C a right angle, AB=6.2 cm and BC=4.5 cm.
View SolutionIf a circle is inscribed in right angled triangle ABC with right angle at B, show that the diameter of the circle is equal to AB+BC−AC.
View Solutionएक समकोण त्रिभुज ABC में, ∠C समकोण है | तथा AC=√3⋅BC हो तो सिद्ध कीजिए कि, ∠ABC=60∘
View Solutionएक समकोण त्रिभुज ABC में, ∠C समकोण है | तथा AC=√3⋅BC हो तो सिद्ध कीजिए कि, ∠ABC=60∘
View SolutionΔABC की भुजाएँ AB=9cm,BC=40cm तथा AC=41cm है दीखाये कि त्रिभुज ABC एक समकोण त्रिभुज है । समकोण का नाम लिखें ।
View Solutionin triangle ABC, B is the right angle. AB = 24cm, BC = 7cm but find these. sin c, cos c
View SolutionABC एक त्रिभुज है जिसका कोण C एक समकोण है। यदि AB = 25 cm तथा AC = 7 cm तब BC ज्ञात कीजिए।
View SolutionIn a right -angled triangle ABC, right-angled at B, if AB=2√6andAC−BC=2, then find secA+tanA.
View SolutionABC is a right angled triangle at A. AD⊥BC, AB=5cm. BC=13cm, AC=12cm. find area of △ABC.
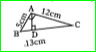
View SolutionABC is a right angle triangle right angled at C. If angle A= 60° and AC= 6cm . Find CB and AB.
View Solution